-
Notifications
You must be signed in to change notification settings - Fork 301
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Merge pull request #317 from AmrutaJayanti/Scikit
Added Scikit Learn Module
- Loading branch information
Showing
1 changed file
with
229 additions
and
0 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,229 @@ | ||
| # Scikit-Learn | ||
|
|
||
| > Unlock the Power of Machine Learning with Scikit-learn: Simplifying Complexity, Empowering Discovery | ||
|
|
||
| **Supervised Learning** | ||
| - Linear Models | ||
|
|
||
| - Support Vector Machines | ||
|
|
||
| - Data Preprocessing | ||
|
|
||
| 1. Linear Models | ||
|
|
||
| The following are a set of | ||
| methods intended for regression in which the target value is expected to | ||
| be a linear combination of the features. In mathematical notation, if | ||
| $\hat{y}$ is the predicted value. | ||
|
|
||
| $$ | ||
| \hat{y}(w, x) = w_0 + w_1 + \ldots + w_p | ||
| $$ | ||
|
|
||
| Across the module, we designate the vector w = | ||
| $(w_0, w_1, \ldots, w_n)$ as `coef_` and $w_0$ as `intercept_`. | ||
|
|
||
|
|
||
| - *Linear Regression* | ||
| Linear Regression fits a linear model with coefficients w = $(w_0 ,w_1 , | ||
| ...w_n)$ to minimize the residual sum of squares between the observed | ||
| targets in the dataset, and the targets predicted by the linear | ||
| approximation. Mathematically it solves a problem of the form: | ||
|
|
||
| $\min_{w} || X w - y||_2^2$ | ||
|
|
||
| ``` python | ||
| from sklearn import linear_model | ||
| reg = linear_model.LinearRegression() #To Use Linear Regression | ||
| reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) | ||
| coefficients = reg.coef_ | ||
| intercept = reg.intercept_ | ||
|
|
||
| print("Coefficients:", coefficients) | ||
| print("Intercept:", intercept) | ||
| ``` | ||
|
|
||
| Output: | ||
|
|
||
| Coefficients: [0.5 0.5] | ||
| Intercept: 1.1102230246251565e-16 | ||
|
|
||
|
|
||
| 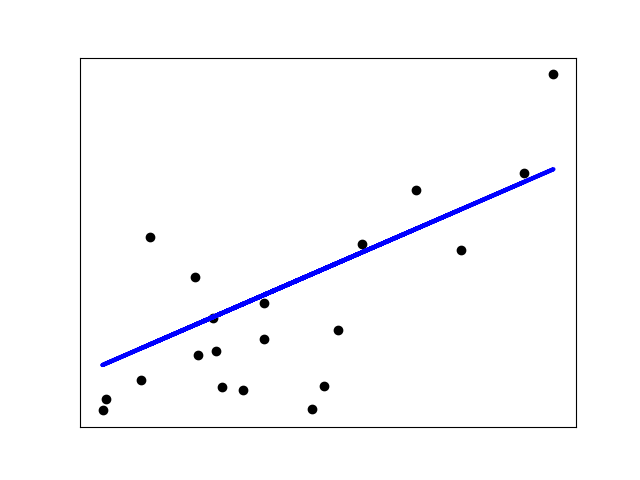 | ||
|
|
||
| This is how the Linear Regression fits the line . | ||
|
|
||
|
|
||
| - Support Vector Machines | ||
| Support vector machines (SVMs) are a set of supervised learning methods | ||
| used for classification, regression and outliers detection. | ||
|
|
||
| *The advantages of support vector machines are:* | ||
|
|
||
| Effective in high dimensional spaces. | ||
|
|
||
| Still effective in cases where number of dimensions is greater than the | ||
| number of samples. | ||
|
|
||
| Uses a subset of training points in the decision function (called | ||
| support vectors), so it is also memory efficient. | ||
|
|
||
| Versatile: different Kernel functions can be specified for the decision | ||
| function. Common kernels are provided, but it is also possible to | ||
| specify custom kernels. | ||
|
|
||
| *The disadvantages of support vector machines include:* | ||
|
|
||
| If the number of features is much greater than the number of samples, | ||
| avoid over-fitting in choosing Kernel functions and regularization term | ||
| is crucial. | ||
|
|
||
| SVMs do not directly provide probability estimates, these are calculated | ||
| using an expensive five-fold cross-validation (see Scores and | ||
| probabilities, below). | ||
|
|
||
| The support vector machines in scikit-learn support both dense | ||
| (numpy.ndarray and convertible to that by numpy.asarray) and sparse (any | ||
| scipy.sparse) sample vectors as input. However, to use an SVM to make | ||
| predictions for sparse data, it must have been fit on such data. For | ||
| optimal performance, use C-ordered numpy.ndarray (dense) or | ||
| scipy.sparse.csr_matrix (sparse) with dtype=float64 | ||
|
|
||
| **Linear Kernel:** | ||
|
|
||
| Function: 𝐾 ( 𝑥 , 𝑦 ) = 𝑥 𝑇 𝑦 | ||
|
|
||
| Parameters: No additional parameters. | ||
|
|
||
| **Polynomial Kernel:** | ||
|
|
||
| Function: 𝐾 ( 𝑥 , 𝑦 ) = ( 𝛾 𝑥 𝑇 𝑦 𝑟 ) 𝑑 | ||
|
|
||
| Parameters: | ||
|
|
||
| γ (gamma): Coefficient for the polynomial term. Higher values increase | ||
| the influence of high-degree polynomials. | ||
|
|
||
| r: Coefficient for the constant term. | ||
|
|
||
| d: Degree of the polynomial. | ||
|
|
||
| **Radial Basis Function (RBF) Kernel:** | ||
|
|
||
| Function: 𝐾 ( 𝑥 , 𝑦 ) = exp ( − 𝛾 ∣ ∣ 𝑥 − 𝑦 ∣ ∣ 2 ) | ||
|
|
||
| Parameters: 𝛾 γ (gamma): Controls the influence of each training | ||
| example. Higher values result in a more complex decision boundary. | ||
|
|
||
| **Sigmoid Kernel:** | ||
|
|
||
| Function: 𝐾 ( 𝑥 , 𝑦 ) = tanh ( 𝛾 𝑥 𝑇 𝑦 𝑟 ) | ||
|
|
||
| Parameters: | ||
|
|
||
| γ (gamma): Coefficient for the sigmoid term. | ||
|
|
||
| r: Coefficient for the constant term. | ||
|
|
||
|
|
||
| ``` python | ||
| import numpy as np | ||
| import matplotlib.pyplot as plt | ||
| from sklearn import svm, datasets | ||
|
|
||
| # Load example dataset (Iris dataset) | ||
| iris = datasets.load_iris() | ||
| X = iris.data[:, :2] # We only take the first two features | ||
| y = iris.target | ||
|
|
||
| # Define the SVM model with RBF kernel | ||
| C = 1.0 # Regularization parameter | ||
| gamma = 0.7 # Kernel coefficient | ||
| svm_model = svm.SVC(kernel='rbf', C=C, gamma=gamma) | ||
|
|
||
| # Train the SVM model | ||
| svm_model.fit(X, y) | ||
|
|
||
| # Plot the decision boundary | ||
| x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 | ||
| y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 | ||
| xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), | ||
| np.arange(y_min, y_max, 0.02)) | ||
| Z = svm_model.predict(np.c_[xx.ravel(), yy.ravel()]) | ||
| Z = Z.reshape(xx.shape) | ||
|
|
||
| plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8) | ||
|
|
||
| # Plot the training points | ||
| plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired) | ||
| plt.xlabel('Sepal length') | ||
| plt.ylabel('Sepal width') | ||
| plt.title('SVM with RBF Kernel') | ||
| plt.show() | ||
| ``` | ||
|  | ||
|
|
||
| - Data Preprocessing | ||
| Data preprocessing is a crucial step in the machine learning pipeline | ||
| that involves transforming raw data into a format suitable for training | ||
| a model. Here are some fundamental techniques in data preprocessing | ||
| using scikit-learn: | ||
|
|
||
| **Handling Missing Values:** | ||
|
|
||
| Imputation: Replace missing values with a calculated value (e.g., mean, | ||
| median, mode) using SimpleImputer. Removal: Remove rows or columns with | ||
| missing values using dropna. | ||
|
|
||
| **Feature Scaling:** | ||
|
|
||
| Standardization: Scale features to have a mean of 0 and a standard | ||
| deviation of 1 using StandardScaler. | ||
|
|
||
| Normalization: Scale features to a range between 0 and 1 using | ||
| MinMaxScaler. Encoding Categorical Variables: | ||
|
|
||
| One-Hot Encoding: Convert categorical variables into binary vectors | ||
| using OneHotEncoder. | ||
|
|
||
| Label Encoding: Encode categorical variables as integers using | ||
| LabelEncoder. | ||
|
|
||
| **Feature Transformation:** | ||
|
|
||
| Polynomial Features: Generate polynomial features up to a specified | ||
| degree using PolynomialFeatures. | ||
|
|
||
| Log Transformation: Transform features using the natural logarithm to | ||
| handle skewed distributions. | ||
|
|
||
| **Handling Outliers:** | ||
|
|
||
| Detection: Identify outliers using statistical methods or domain | ||
| knowledge. Transformation: Apply transformations (e.g., winsorization) | ||
| or remove outliers based on a threshold. | ||
|
|
||
| **Handling Imbalanced Data:** | ||
|
|
||
| Resampling: Over-sample minority class or under-sample majority class to | ||
| balance the dataset using techniques like RandomOverSampler or | ||
| RandomUnderSampler. | ||
|
|
||
| Synthetic Sampling: Generate synthetic samples for the minority class | ||
| using algorithms like Synthetic Minority Over-sampling Technique | ||
| (SMOTE). Feature Selection: | ||
|
|
||
| Univariate Feature Selection: Select features based on statistical tests | ||
| like ANOVA using SelectKBest or SelectPercentile. | ||
|
|
||
| Recursive Feature Elimination: Select features recursively by | ||
| considering smaller and smaller sets of features using RFECV. | ||
|
|
||
| **Splitting Data:** | ||
|
|
||
| Train-Test Split: Split the dataset into training and testing sets using | ||
| train_test_split. | ||
|
|
||
| Cross-Validation: Split the dataset into multiple folds for | ||
| cross-validation using KFold or StratifiedKFold. |