First created in 2015 (last updated 2021), this is a prototype of an automatic hyperbolic art generator and educational tool. It creates a regular edge to edge tiling of the hyperbolic plane represented as a Poincaré disk, also known as a hyperbolic tesselation.
These were originally described by H. S. M. Coxeter, but were made famous by M.C. Escher in his series of Circle Limit woodcuts, back in the era when people were known only by their initials and surnames.
Currently it can create images similar to Escher’s Circle Limit I. These are regular two colored tilings, defined by the number of sides of the polygons, and the number of polygons that meet at each vertex.
The tiling is created out out of two Euclidean triangular pieces, one representing half a white fish, the other half a black fish.
The final result will look something like this (this one is a {6,6} tiling):
I had originally planned to extend this to include irregular tilings of several colors, and then to use this as a teaching tool where students could create their own tiles.
Unfortunately, creating the tiles so that they match evenly turned out to be more difficult than I expected. It’s quite unintuitive since the Euclidean triangles get stretched to map onto hyperbolic triangles, and the lines of opposing edges don’t match up where you would expect. Since the idea was to create a simple educational tool where students could quickly create their own designs, this was a bit of a showstopper, and I halted development.
Note that once you go over around 8 for either values the polygons will start to get very stretched at the edges.
A current tiling consists of around 50,000 hyperbolic polygons, each built out of hundreds of regular polygons. In general, a tiling can be generated in 50 milliseconds or so.
This way this works by mapping the two triangular images to hyperbolic triangles (a non-affine texture mapping), and then covering the central polygon with them. Then this central polygon is appropriately rotated and repeated until the entire plane is covered.
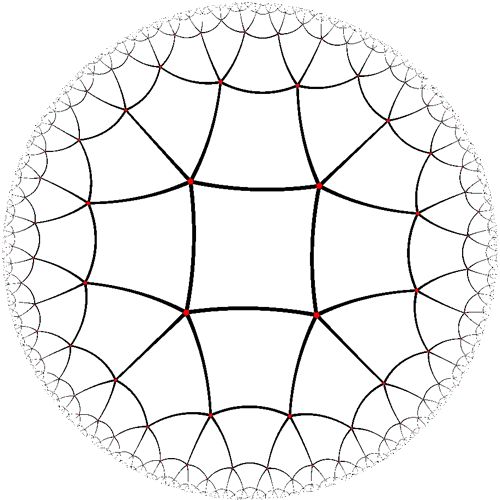
The following figure is a {4, 5} tiling - that means 4 sided polygons, with 5 meeting at each vertex.
The algorithm used was first described by Douglas Dunham and as far as I can tell first implemented in software by his PHD student Ajit Datar.
However, this was probably the first implementation using JavaScript and WebGL when I first created it in 2015.
If you are interested in reading more about hyperbolic tesselation, check out the Dr. Dunham’s homepage linked above, or for a slightly gentler introduction, try this page by Prof. Joyce at Clare university, as well the wikpedia page.
Prerequisites: Node.js
- Clone or download the repo
- Open a terminal and run
npm install - Once all packages have installed, run
npm start - Open a web browser and navigate to http://localhost:8080 or one of the other addresses logged in the terminal