John MacAuley, ESnet
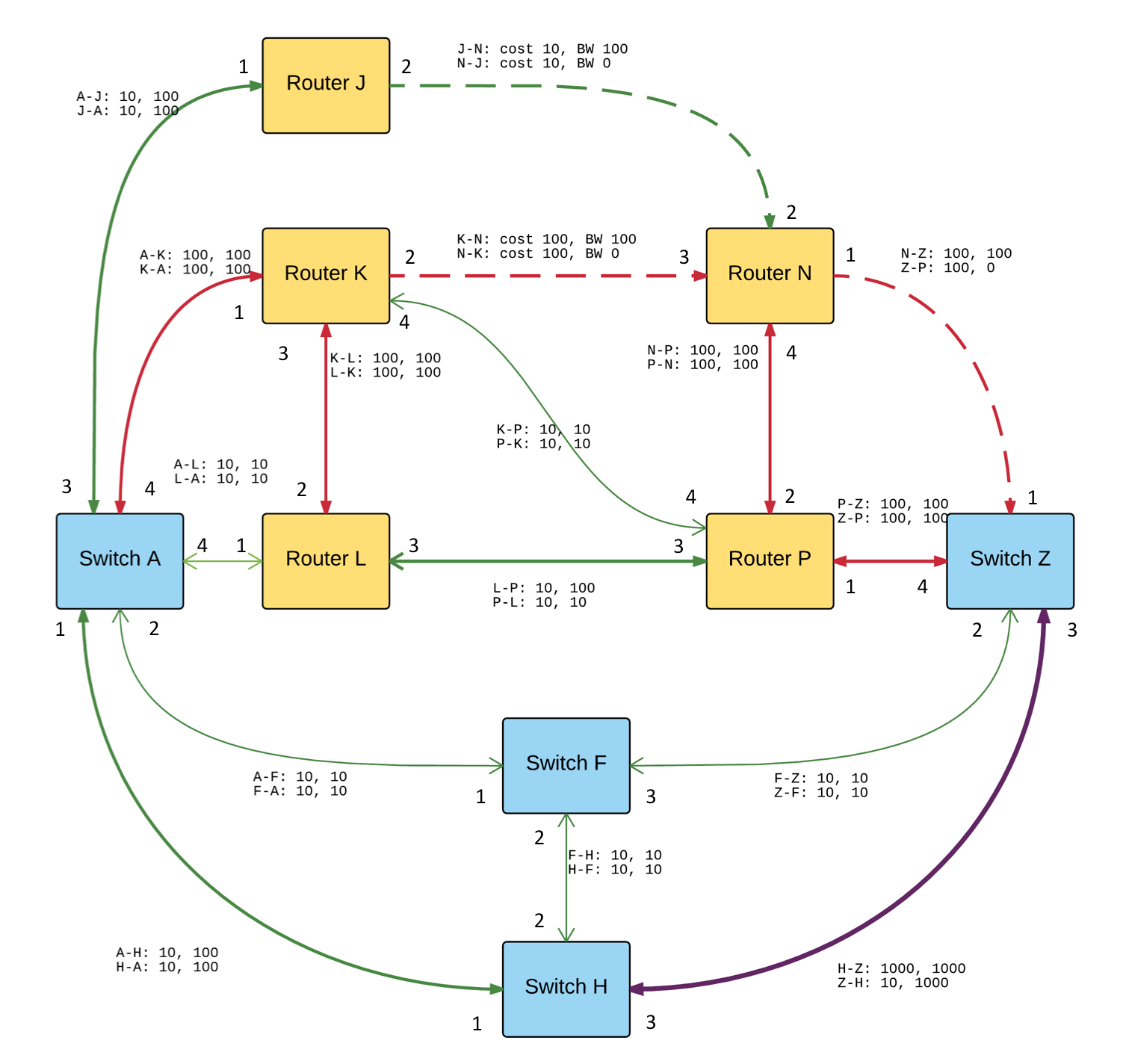
Vangelis presented a pathfinding problem he was encountering in the rewrite of ESnet's OSCARS SDN controller - How to find a lowest cost path through the ESnet network where there is a mixture of Ethernet and MPLS links each with different connection characteristics? Connection segments using Ethernet links must be bidirectional - asymmetric bandwidth with symmetric paired link segments. Connection segments using MPLS links can consist of unidirectional segments following different network paths while composing an overall bidirectional flow. The following diagram shows the reference network with cost and bandwidth available on each link.
I always try to solve these types of pathfinding problems using a standard Dijkstra shortest path algorithm with a graph that models any specific restrictions of the problem space. Vangelis didn't think it could be done. That was good enough to motivate me. Challenge accepted!
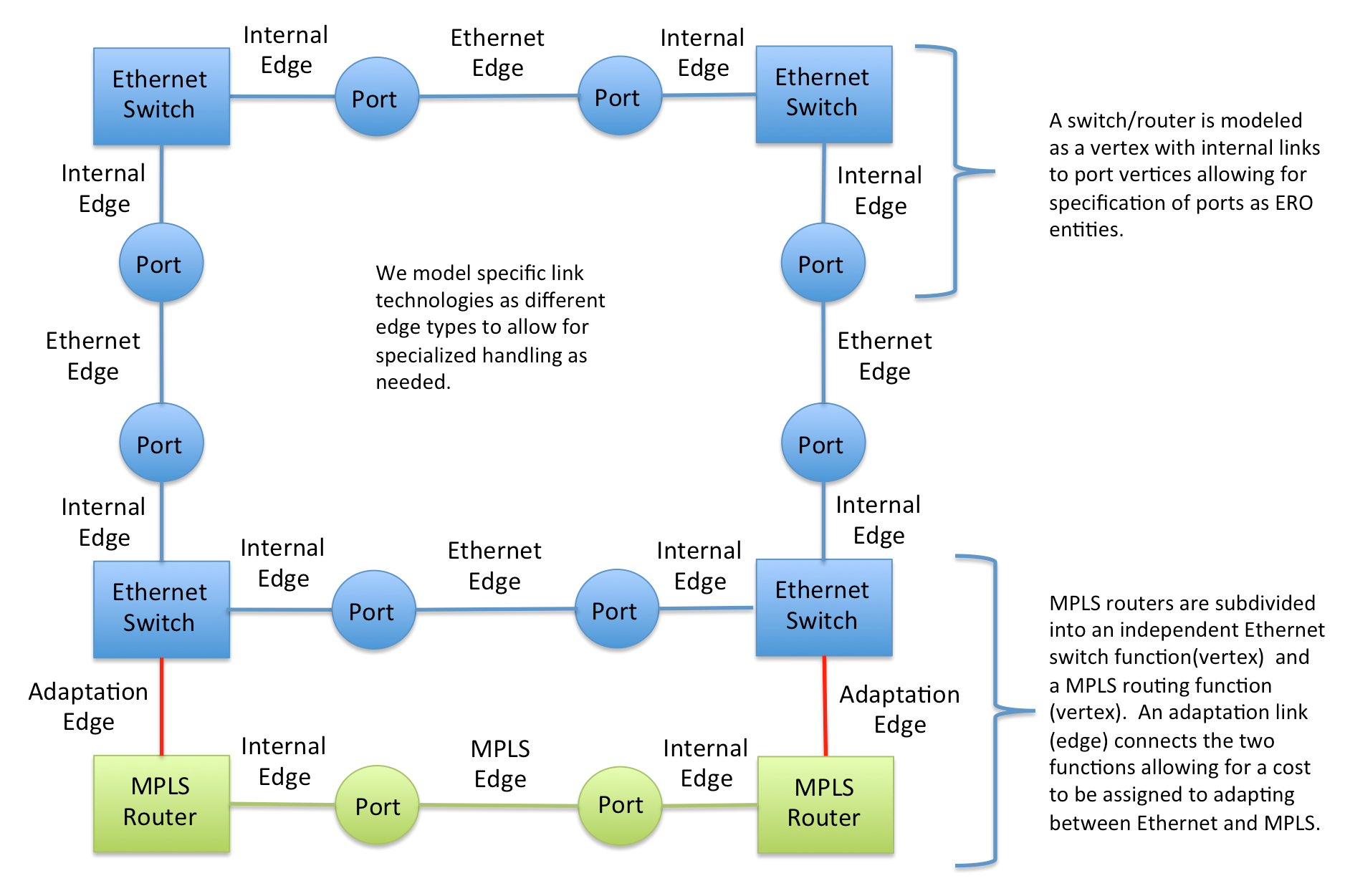
First thing I did was separate the routers into an Ethernet switch, adaptation, and MPLS router components. This allowed a clear separation of networking capabilities, and simplified the components to perform a single function. I then built a conceptual graph that looked like the following diagram:
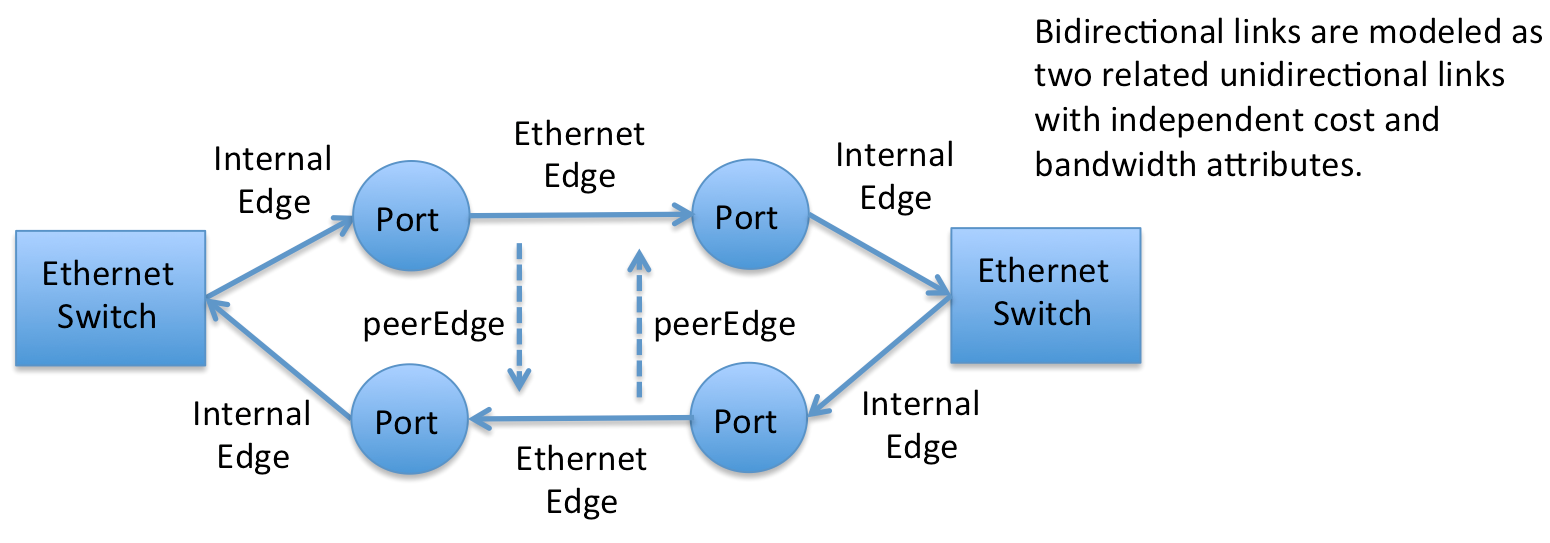
Although I started using bidirectional edges within the graph I changed to using unidirectional edges with references to the peer link in the bidirectional pair. This allowed for a simplification in modelling.
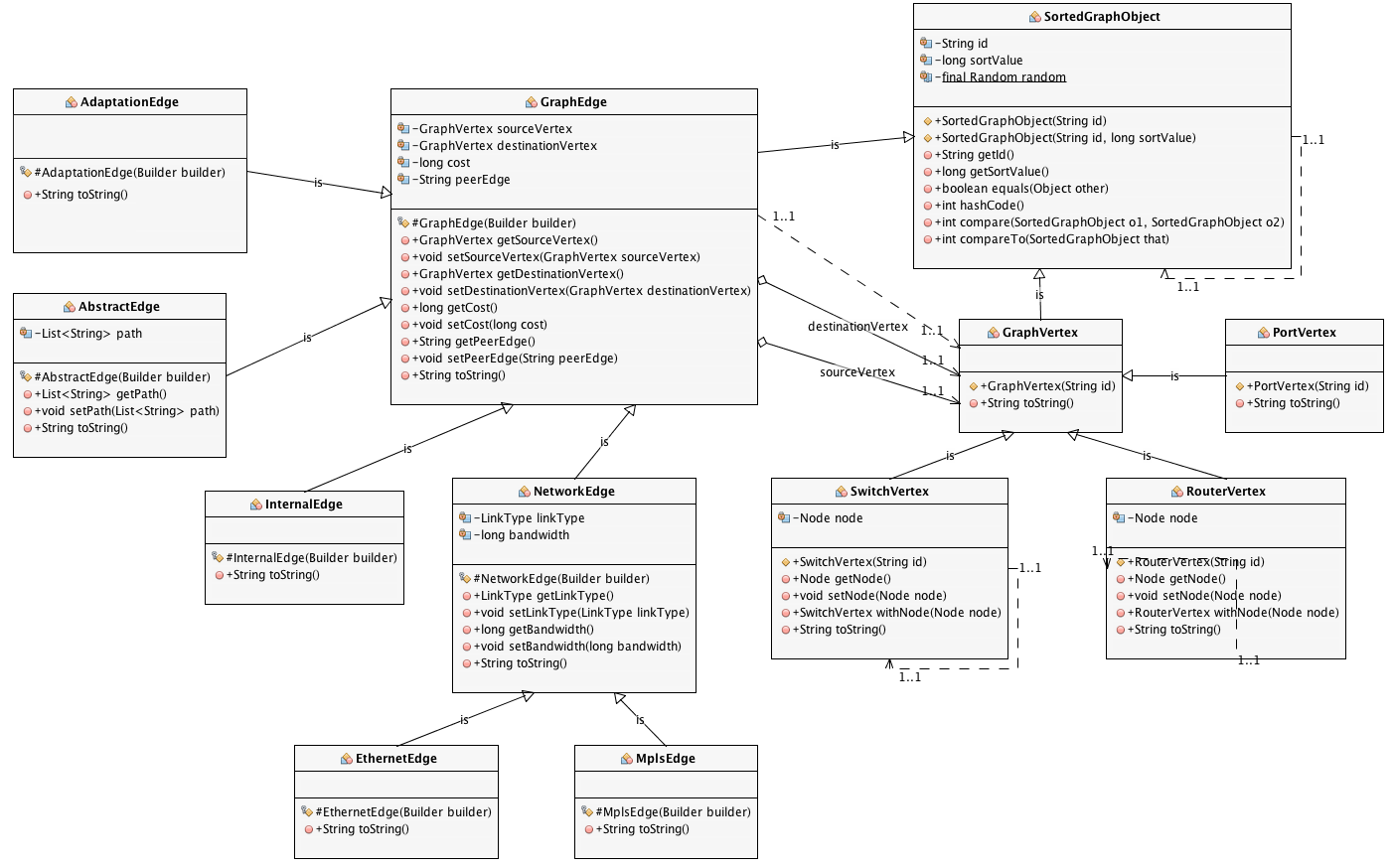
Although the class model could be simplified with a refactoring, this is the model currently being used in the code:
The root object in this graph model is the SortedGraphObject that provides each object with a randomized long value used within the sorted graph to vary the path results when multiple equal paths have been computed. The default algorithm for the Jung graph is to return the lowest cost path based on the first inserted node/edge. As implemented this graph will randomize the result. The remaining objects are described below.
As a start I created a flat unidirectional graph to determine optimal unidirectional flows. Unidirectional Ethernet links (paired for bidirectionally) were modelled between all Ethernet switches. A pair of adaptation links between each Ethernet switch and associated MPLS router was added to connect the two technologies and allow a cost to be assigned to the act of adaptation. MPLS routers were connected using MPLS links also paired for bidirectionally. The FlatMultiGraphPCE class builds this graph and implements both independent unidirectional path computation (using the UnidirectionalEdgeEvaluator), as well as bidirectional path computation using paired edges (using the BidirectionalEdgeEvaluator).
Within this unidirectional graph I perform pathfinding in one direction (source to destination). For unidirectional connections this is straight forward, however, for bidirectional symmetric path connections it requires additional logic. In the one-pass bidirectional path algorithm each time we visit an edge to determine viability we validate the peered unidirectional edge has sufficient bandwidth to handle the return path. If the bidirectional edge pair do meet the connection criteria then we sum the cost of the two edges and return this blended cost as the cost of the edge being evaluated. If not then we invalidate this edge. Here us the logic being performed in the BidirectionalEdgeEvaluator:
if (request.outboundBandwidth > edge.bandwidth) {
return INVALID;
}
if (request.inboundBandwidth > peerEdge.bandwidth) {
return INVALID;
}
return edge.cost + peerEdge.cost;
Once Dijkstra has completed the source to destination path computation we have already validated the reverse path as well. The shortest path is then the path consisting of the set of edges with the lowest total sum of individual costs. Below are the results of pathfinding on this graph. The request is for a path between SwA and SwZ with outbound bandwidth of 100 and inbound bandwidth of 10. Notice the individual unidirectional path results are quite different than the bidirectional (symmetric) path results.
Unidirectional path: source=SwA, destination=SwZ, bandwidth=100
SwA:3-to-SwJ:1
SwJ-to-RtJ
RtJ:2-to-RtN:2
RtN-to-SwN
SwN:1-to-SwZ:1
Length=5, returned cost=120, total cost=120
Unidirectional path: source=SwZ, destination=SwA, bandwidth=10
SwZ:3-to-SwH:3
SwH:1-to-SwA:1
Length=2, returned cost=20, total cost=20
Bidirectional path: source=SwA, destination=SwZ, outbound=100, inbound=10
Outbound path:
SwA:4-to-SwK:1
SwK-to-RtK
RtK:3-to-RtL:2
RtL:3-to-RtP:3
RtP-to-SwP
SwP:1-to-SwZ:4
Inbound path:
SwZ:4-to-SwP:1
SwP-to-RtP
RtP:3-to-RtL:3
RtL:2-to-RtK:3
RtK-to-SwK
SwK:1-to-SwA:4
Outbound path length=6, cost=310
Inbound path length=6, cost=310
Average cost=310
Now we need to consider how to perform pathfinding in such a way as to restrict a bidirectional connection to use bidirectional symmetric path segments on Ethernet edges, but is free to use independent unidirectional path segments on MPLS edges. In this case we still sum the costs of the paired Ethernet edges as was done above, but need to minimize the cost of the MPLS edges used by evaluating individual unidirectional path segments. Below is the optimal path for the requested path given the independent unidirectional path segments on MPLS edges.
Bidirectional path: source=SwA, destination=SwZ, outbound=100, inbound=10
Outbound path:
SwA:4-to-SwK:1
SwK-to-RtK
RtK:3-to-RtL:2
RtL:3-to-RtP:3
RtP-to-SwP
SwP:1-to-SwZ:4
Inbound path:
SwZ:4-to-SwP:1
SwP-to-RtP
RtP:4-to-RtK:4
RtK-to-SwK
SwK:1-to-SwA:4
Outbound path length=6, cost=310
Inbound path length=5, cost=210
Average cost=260
As you can see the chosen optimal path is different than a straight bidirectional path since a combination of cheaper lower cost MPLS edges can be used once the symmetric edge restriction is dropped for the MPLS segments. To help compute this optimal path while still using Jung's off-the-shelf Dijkstra algorithm I subdivided the network into two separate graphs creating a layered network hierarchy. This allows different routing behaviours to be defined for each technology.
The first graph represented the upper layer Ethernet network. Unidirectional Ethernet links (paired for bidirectionally) were modelled between all Ethernet switches. A pair of adaptation links between each Ethernet switch and associated MPLS router was added to connected the two technologies and model any cost associated with the adaptation. In this Ethernet graph we do not model MPLS links, but instead an abstract link. Each MPLS router is connected to every other MPLS router via an abstract edge representing the potential for an MPLS link not the actual existence of one. Effectively, this graph looked identical to the flat unidirectional graph except for the use of abstract edges between MPLS routers, and the added full mesh of edges between these routers. The second graph holds the MPLS routers and the real MPLS links between these routers.
The AbstractMultiGraphPCE class builds this graph and implements both independent unidirectional path computation (using the AbstractUniEdgeEvaluator), as well as bidirectional path computation using paired edges (using the AbstractBiEdgeEvaluator).
All pathfinding is initiated on the Ethernet graph (since we are pathfinding for Ethernet services). I use the Jung edge transformer function to assign a weight to each edge in the graph as Dijkstra visits these edges. For bidirectional connections we follow the same logic as in the flat graph to make sure both unidirectional Ethernet edges have the required bandwidth. Weights for a bidirectional link are computed by the edge transformer as the sum of the cost of both unidirectional links using the paired edge logic:
if (request.outboundBandwidth > edge.bandwidth) {
return INVALID;
}
if (request.inboundBandwidth > peerEdge.bandwidth) {
return INVALID;
}
return edge.cost + peerEdge.cost;
When the edge transformer encounters an abstract edge within the Ethernet graph we do some additional pathfinding using the second MPLS graph. Using the source and destination MPLS router on the abstract link I perform independent unidirectional path fining to determine the cheapest two paths for this abstract link. The cost of the abstract link is then the sum of these two independent MPLS unidirectional paths. The paths returned from the MPLS graph are now stored in the associated abstract link for later use. If a path is not found the standard invalid edge behaviour is maintained.
if (edge instanceof AbstractEdge) {
// Get associated peer abstract edge.
AbstractEdge ab = (AbstractEdge) edge;
GraphEdge peerEdge = edgeMap.get(ab.getPeerEdge());
if (peerEdge == null || !(peerEdge instanceof AbstractEdge)) {
return INVALID;
}
// This is an "abstract link" requiring us to perform pathfinding
// on the underlying MPLS graph.
UnidirectionalResult outboundResult =
mplsGraph.computeUnidirectionalPath(ab.getSourceVertex().getId(),
ab.getDestinationVertex().getId(), outboundBandwidth);
UnidirectionalResult inboundResult =
mplsGraph.computeUnidirectionalPath(ab.getDestinationVertex().getId(),
ab.getSourceVertex().getId(), inboundBandwidth);
// Save the actual path and cost of the underlying MPLS path.
ab.setPath(outboundResult.getPath());
ab.setCost(outboundResult.getCost());
((AbstractEdge) peerEdge).setPath(inboundResult.getPath());
peerEdge.setCost(inboundResult.getCost());
// If either of the unidirectional paths were not possible then this
// is not a feasible path.
if (outboundResult.getPath().isEmpty() || inboundResult.getPath().isEmpty()) {
return INVALID;
}
return inboundResult.getCost() + outboundResult.getCost();
}
Dijkstra will correctly choose the optimal path using this layered two graph mechanism. Since we have separated the Ethernet and MPLS pathfinding into separate graphs it is possible to support different behaviours for each graph (bidirectional versus unidirectional). This allows for simplification of the algorithm logic while still achieving the desired outcome.
Running Dijkstra on the MPLS graph would give the outbound abstract edge an MPLS path (RtK -> RtL -> RtP) at a cost of 110, while the inbound path would be (RtP -> RtK) at a cost of 10. This gives the abstract edge a cost of 120 during bidirectional evaluation.
When I unwind the returned Ethernet path to include a complete MPLS path I look into the "path" member of the abstract edge to pull out the MPLS details I stored inside while evaluating the edge cost. Poof you are done!
Yes the hierarchical graph approach is costly specifically around the path computation on the abstract links. However, this can be optimized in Jung through caching of state in the DijkstraShortestPath algorithm so that iterative getPath() calls will reuse previously computed tables. I am sure there are other optimizations that can lead to similar performance improvements.