HAL-CGP

Cartesian genetic programming (CGP) in pure Python.

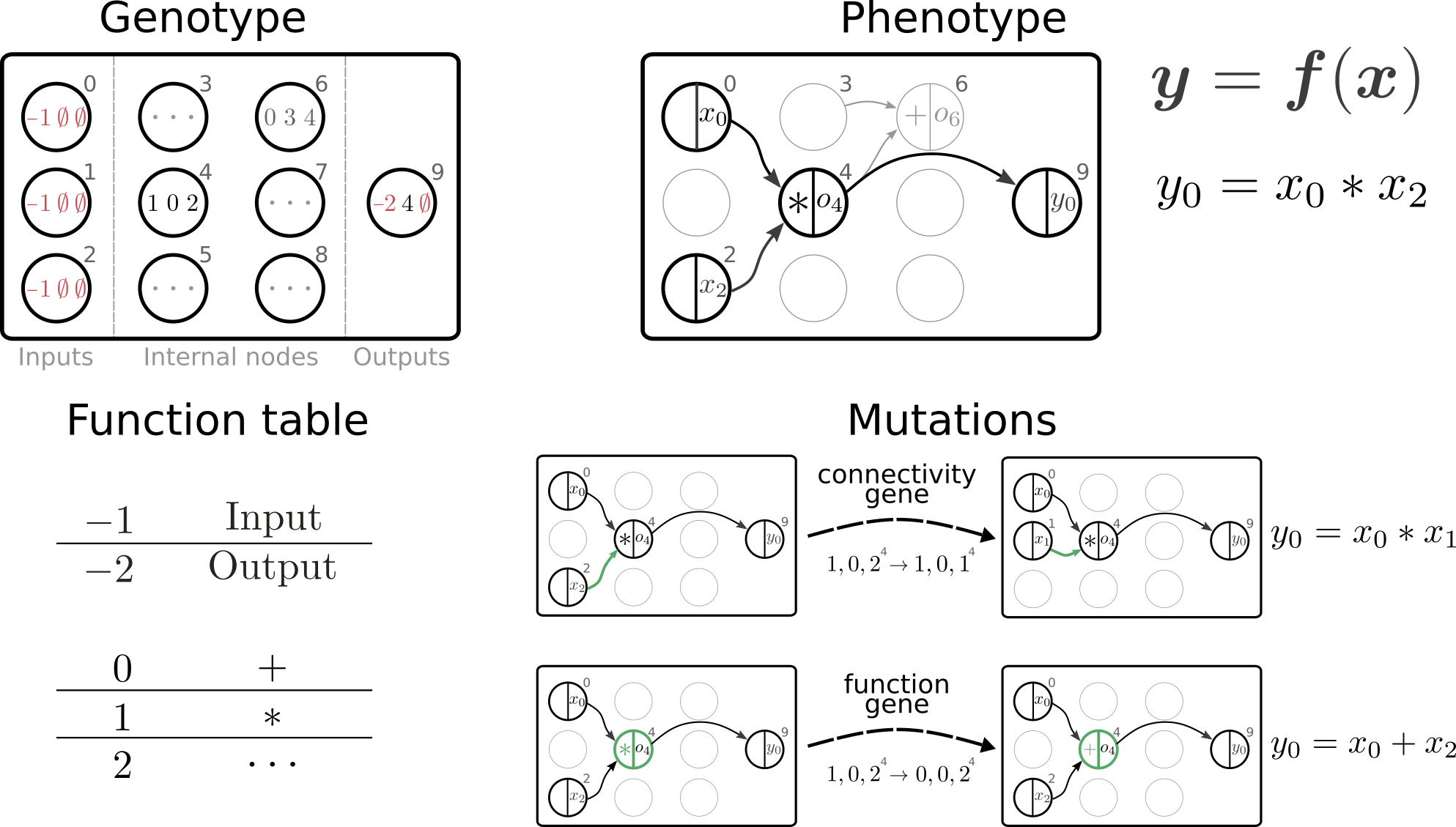
This library implements Cartesian genetic programming (e.g, Miller and Thomson, 2000; Miller, 2011) for symbolic regression in pure Python, targeting applications with expensive fitness evaluations. It provides Python data structures to represent and evolve two-dimensional directed graphs (genotype) that are translated into computational graphs (phenotype) implementing mathematical expressions. The computational graphs can be compiled as a Python functions, SymPy expressions (Meurer et al., 2017) or PyTorch modules (Paszke et al., 2017). The library currently implements an evolutionary algorithm, specifically (mu + lambda) evolution strategies adapted from Deb et al. (2002), to evolve a population of symbolic expressions in order to optimize an objective function.

_{Figure from Jordan, Schmidt, Senn & Petrovici, "Evolving to learn: discovering interpretable plasticity rules for spiking networks", arxiv:2005.14149.}

A simple example of CGP applied to a symbolic regression problem can be found in examples/example_evo_regression.py.

Searching numerical values for constants via local search

This library supports the use of constants as operator nodes in order to represent expressions like f(x) = x + c with some fixed value c. While the ConstantFloat node and derived nodes have a fixed output value, the output value of Parameter nodes are stored per individual and hence can be modified during evolution via local search. The library provides a local search function that performs stochastic gradient descent on the values of Parameter nodes (cf. Topchy & Punch, 2001; Izzo et al., 2017). See examples/example_differential_evo_regression.py for an example evolving an expression containing mathematical constants.

Basic usage

Follow these steps to solve a basic regression problem:

1. Define an objective function. The objective function takes an individual as an argument and updates the fitness of the individual.

def objective(individual):
    individual.fitness = ...
    return individual

2. Define parameters for the population, the genome, the evolutionary algorithm and the evolve function.

population_params = {"n_parents": 10, "mutation_rate": 0.5, "seed": 8188211}

genome_params = {
	"n_inputs": 2,
	"n_outputs": 1,
	"n_columns": 10,
	"n_rows": 2,
	"levels_back": 5,
	"primitives": (cgp.Add, cgp.Sub, cgp.Mul, cgp.Div, cgp.ConstantFloat),
}

ea_params = {"n_offsprings": 10, "n_breeding": 10, "tournament_size": 2, "n_processes": 2}

evolve_params = {"max_generations": 1000, "min_fitness": 0.0}

3. Initialize a population and an evolutionary algorithm instance:

pop = cgp.Population(**population_params, genome_params=genome_params)
ea = cgp.ea.MuPlusLambda(**ea_params)

4. Define a callback function to record information about the progress of the evolution:

history = {}
history["fitness_parents"] = []
def recording_callback(pop):
	history["fitness_parents"].append(pop.fitness_parents())

5. Use the evolve function that ties everything together and executes the evolution:

cgp.evolve(pop, obj, ea, **evolve_params, print_progress=True, callback=recording_callback)

References

Miller, J. and Thomson, P. (2000). Cartesian genetic programming. In Proc. European Conference on Genetic Programming, volume 1802, pages 121-132. Springer.

Miller, J. F. (2011). Cartesian genetic programming. In Cartesian genetic programming, pages 17-34. Springer.

Meurer, A., Smith, C. P., Paprocki, M., Certik, O., Kirpichev, S. B., Rocklin, M., ... & Rathnayake, T. (2017). SymPy: Symbolic Computing in Python. PeerJ Computer Science, 3, e103.

Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E., DeVito, Z., ... & Lerer, A. (2017). Automatic Differentiation in PyTorch.

Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. A. M. T. (2002). A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182-197.

Topchy, A., & Punch, W. F. (2001). Faster Genetic Programming based on Local Gradient Search of Numeric Leaf Values. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2001) (Vol. 155162). Morgan Kaufmann San Francisco, CA, USA.

Izzo, D., Biscani, F., & Mereta, A. (2017). Differentiable Genetic Programming. In European Conference on Genetic Programming (pp. 35-51). Springer, Cham.