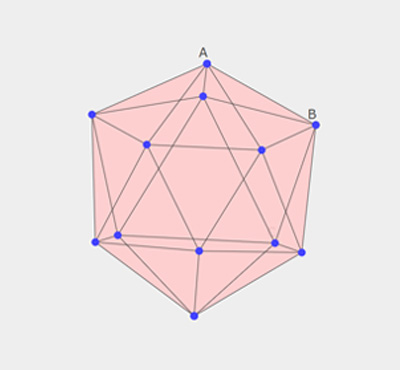
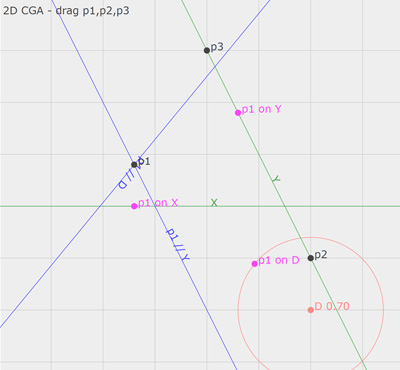
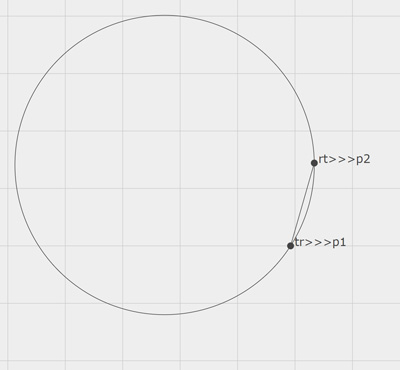
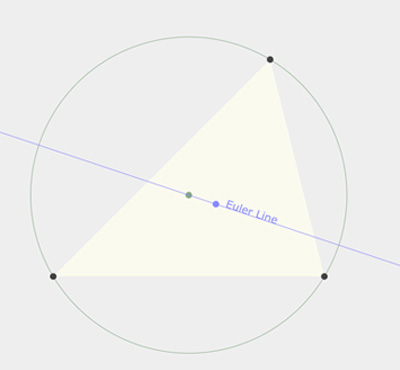
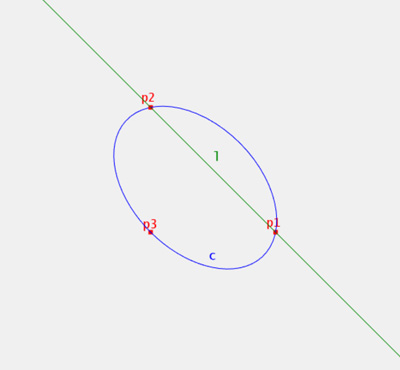
Geometric Algebra - Not Just Algebra
Ganja.js is a Geometric Algebra code generator for javascript. It generates Clifford algebras and sub-algebras of any signature and implements operator overloading and algebraic constants.
cite as
@misc{https://doi.org/10.5281/zenodo.3635774,
doi = {10.5281/ZENODO.3635774},
url = {https://zenodo.org/record/3635774},
author = {De Keninck, Steven},
title = {ganja.js},
publisher = {Zenodo},
year = {2020}
}(Mathematically, an algebra generated by ganja.js is a graded exterior (Grassmann) algebra (or one of its subalgebras) with a non-metric outer product, extended (Clifford) with geometric and contraction inner products, a Poincare duality operator and the main involutions and morphisms.)
(Technically, ganja.js is a code generator producing classes that reificate algebraic literals and expressions by using reflection, a built-in tokenizer and a simple AST translator to rewrite functions containing algebraic constructs to their procedural counterparts.)
(Practically, ganja.js enables real math syntax inside javascript, with element, vector and matrix operations over reals, complex numbers, dual numbers, hyperbolic numbers, vectors, spacetime events, quaternions, dual quaternions, biquaternions or any other Clifford Algebra.)
(Seriously, look at the examples, run some quick numbers using the GAlculator or play the wedge game first.)
Visit bivector.net for our forum and chat - the perfect place for questions and support.
ganja.js now has a nodejs based templated source generator that allows the creation of arbitrary algebras for C++, C#, python and rust. The generated code provides in a flat multivector format and operator overloading. Check the 'codegen' folder for the source, several algebras are available in pregenerated versions.
- C++ pre-generated sources
- C# pre-generated sources
- rust pre-generated sources
- python pre-generated sources
1. Reasons to use ganja
2. Using ganja for the first time
3. Getting free ganja samples
4. Ganja for experienced users
5. Ganja ingredients and syntax
6. Ganja starterkit : PGA2D P(R*2,0,1)
7. Ganja starterkit : PGA3D P(R*3,0,1)
Ganja.js makes doing Geometric Algebra in your browser easy and fun. Its inline syntax and graphing makes math in the browser feel like .. math.
- Operator overloading
- Algebraic constants
- Supports any metric (positive,negative,zero) and dimensionality (also +10)
- smallish (20kb on the wire)
- matrix-free inverses up to 5D.
- geometric, inner (left contraction), outer (wedge) and regressive (vee) product
- conjugate, Reverse, Involute, Dual (Poincare), Negative
- 4 API's (inline, asciimath, object oriented, functional)
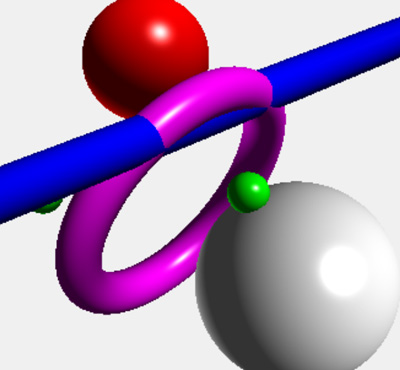
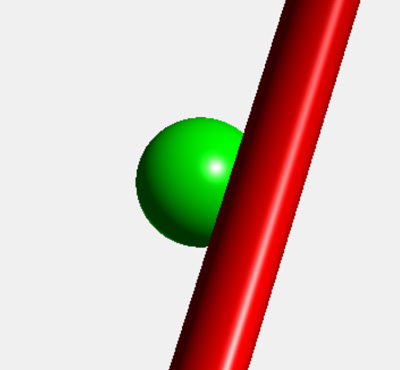
- Easy graph function for 1D and 2D functions, Projective 2D, 3D and conformal 2D and 3D elements. (SVG/webGL/OPNS)
- Supports vectors and matrices in all its algebras.
- There's a game that teaches you how to use ganja.js !
Install ganja.js using npm :
npm install ganja.js
And require it in your script :
var Algebra=require('ganja.js');Or in the browser, just include the ganja.js script. (ganja.js has no dependencies)
<SCRIPT SRC="https://unpkg.com/ganja.js"></SCRIPT>To create an Algebra, call the Algebra function specifying the metric signature (number of positive,negative and zero dimensions). The result is an ES6 class implementing the requested clifford algebra.
function Algebra( p, q, r, func );
// p = number of positive dimensions.
// q = optional number of negative dimensions.
// r = optional number of zero dimensions.
// func = optional function. (shorthand .. it is passed to .inline and executed) An extended syntax is also available that allows you to further tweak the created Algebra.
function Algebra( options, func );
// options = object containing subset of
// {
// p, integer number of positive dimensions.
// q, integer number of negative dimensions.
// r, integer number of zero dimensions.
// metric, [a,b,..] array with metric per generating dimensions. (e.g. [0,1,1] for PGA2D)
// basis, ["1","e1","e2"] basis that overrules the standard cannonical basis.
// Cayley, [["1","e1"],["e1","-1"]] Cayley table to overrule standard GA tables.
// baseType, float32Array (default), float64Array, .. baseType to be used for the Elements.
// mix Set to true to enable interoperable sub-algebras. (defaults to false).
// }
// returns : algebra class if no func supplied, function result if func supplied.Here are some examples :
// Basic
var Hyper = Algebra(1); // Hyperbolic numbers.
var Complex = Algebra(0,1); // Complex numbers.
var Dual = Algebra(0,0,1); // Dual numbers.
var H = Algebra(0,2); // Quaternions.
// Clifford
var Cl2 = Algebra(2); // Clifford algebra for 2D vector space.
var Cl3 = Algebra(3); // Clifford algebra for 3D vector space.
var timeSpace = Algebra(1,3); // Clifford algebra for timespace vectors.
// SubAlgebras
var Complex = Algebra({p:3,basis:['1','e123']}); // Complex Numbers as subalgebra of Cl3
var H = Algebra({p:3,basis:['1','e12','e13','e23']}); // Quaternions as even subalgebra of Cl3
// Geometric
var PGA2D = Algebra(2,0,1); // Projective Euclidean 2D plane. (dual)
var PGA3D = Algebra(3,0,1); // Projective Euclidean 3D space. (dual)
var CGA2D = Algebra(3,1); // conformal 2D space.
var CGA3D = Algebra(4,1); // Conformal 3D space.
// High-Dimensional GA
var DCGA3D = Algebra(6,2); // Double Conformal 3D Space.
var TCGA3D = Algebra(9,3); // Triple Conformal 3D Space.
var DCGSTA = Algebra(4,8); // Double Conformal Geometric Space Time Algebra.
var QCGA = Algebra(9,6); // Quadric Conformal Geometric Algebra. You can now use these classes to generate algebraic elements. Those elements will have all of the expected properties. (Length, blade access, Dot, Wedge, Mul, Dual, Inverse, etc ...)
And while not advised you could use them in a 'classic' programming style syntax like the example below.
var Complex = Algebra(0,1); // Complex numbers.
var a = new Complex([3,2]); // 3+2i
var b = new Complex([1,4]); // 1+4i
return a.Mul(b); // returns [-5, 14]This however, is not very pretty. It's not that much fun either. Luckily, ganja.js provides an alternate way to write algebraic functions, literals and expressions.
Your Algebra class exposes this interface through the inline function. It accepts a javascript function, and translates it to use the Algebra of your choice. Using the inline function, the above example is written :
Algebra(0,1).inline(()=>(3+2e1)*(1+4e1))(); // return [-5,14]Note that if you are immediately executing the function, you can add it as a last parameter to your Algebra constructor call.
Algebra(0,1,()=>(3+2e1)*(1+4e1)); // return [-5,14]The inline syntax is powerful and flexible. It offers full operator overloading, overloads scientific e-notation to allow you to directly specify basis blades and allows using arrays or lambda expressions without the need for calling brackets in algebraic expressions.
Algebra(2,0,1,()={
// Direct specification of basis blades using e-notation.
var xy_bivector = 1e12,
pseudoscalar = 1e012;
// Operator overloading .. * = geometric product, ^ = wedge, & = vee, << = dot, >>> = sandwich ...
var xy_bivector_from_product = 1e1 * 1e2;
// Directly specified point.
var some_point = 1e12 + 0.4e01 + 0.5e02;
// Function that returns point.
var function_that_returns_point = ()=>some_point + 0.5e01;
// Join of point and function .. notice no calling brackets ..
var join_between_point_and_function = some_point & function_that_returns_point;
// Same line as above.. but as function.. (so will update if the point changes)
var function_that_returns_join = ()=>some_point & function_that_returns_point;
// Binary operations on arrays also work as expected.
var even = [1,2,3,4,5]*2;
// Even if those contain multivectors or other arrays :
var funky = [1, 1e01+0.5e02, [3,4]] * 3 + [1,2,3];
// All elements and functions can be rendered directly. (again, no calling brackets).
var canvas = this.graph([ some_point, function_that_returns_point, function_that_returns_join ]);
});Under the hood, ganja.js will translate these functions.
// the pretty mathematical expression (!=dual, ^=wedge)
a = ()=>!(!a^!b)*(c*1e23)
// gets translated to ..
b = ()=>this.Mul(this.Dual((this.Wedge(this.Dual(a),this.Dual(b)))),(this.Mul(c,this.Coeff(6,1))))In the example above, functions a and b do the same thing, but it should be clear that a-b=headeache. Because I'm out of aspirin, I'll leave the proof of that to the reader.
See the coffeeshop for more examples of how to use the inline syntax.
Your Algebra also exposes a static graph function that allows you to easily graph 1D or 2D functions as well as 2D and 3D PGA and CGA elements.
- canvas output is available for 1D and 2D functions.
- SVG output is available for 2D PGA, 3D PGA and 2D CGA.
- webGL output is available for 3D PGA and 3D CGA.
- webGL2 implicit OPNS rendering is available for all other spaces.
canvas = Algebra(0).graph(x=>Math.sin(x*5)); // Graph a 1D function in R
canvas = Algebra(0).graph((x,y)=>x+y); // Graph a 2D function in R
svg = Algebra(2,0,1,()=>this.graph([1e12,1e1,1e2])); // Graph the origin and x and y-axis in 2D PGA
svg = Algebra(3,0,1,()=>this.graph([1e123,1e23,1e13,1e12],{camera:1+.5e01-.5e02})); // and in 3D PGA
canvas = Algebra(4,1,()=>this.graph([.5e4-.5e5],{conformal:true,gl:true}); // The origin in 3D CGAAgain, many more examples can be found at the coffeeshop.
To display the basis blade names, metric, Cayley table and more, use the static describe function.
Algebra(0,1).describe();sample output :
Basis
1,e1
Metric
-1
Cayley
1, e1
e1, -1
Matrix Form:
A,-B
B, A
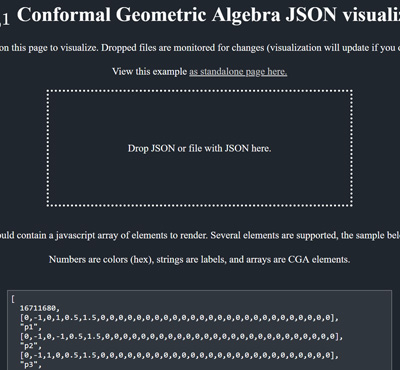
Please visit the coffeeshop and play around with the examples. They are interactive and you can easily change the code online. No need to download or install anything !
complex mandelbrot
|
complex least squares
|
dual differentiation
|
dual backpropagation
|
quaternion hue
|
quaternion mandelbrot
|
timespace lorentz
|
pga2d points and lines
|
pga2d distances and angles
|
pga2d project and reject
|
pga2d rotors and translators
|
pga2d isometries
|
pga2d inverse kinematics
|
pga2d separating axis
|
pga2d pose estimation
|
pga2d euler line
|
pga2d desargues theorem
|
pga2d differentiation
|
pga2d physics moon
|
pga2d origami
|
pga2d poncelet
|
pga3d points and lines
|
pga3d distances and angles
|
pga3d rotors and translators
|
pga3d icosahedron
|
pga3d sampling
|
pga3d slicing
|
pga3d differentiation
|
pga3d skinning
|
pga3d physics planets
|
pga3d origami
|
pga3d physics symmetric top
|
pga3d physics free top
|
pga3d objects
|
cga2d points and circles
|
cga2d project and reject
|
cga2d rotors and translators
|
cga2d euler line
|
cga3d points circles lines
|
cga3d points spheres planes
|
cga3d dual spheres planes
|
cga3d intersections
|
cga3d project reject
|
cga3d opns visualizer
|
cga3d opns line circle
|
cga3d json
|
mga3d points and lines
|
ccga3d points quadrics
|
qcga3d points and more
|
game wedge
|
ganja.js is also the engine behind the GAlculator - try it online or get it on the play store
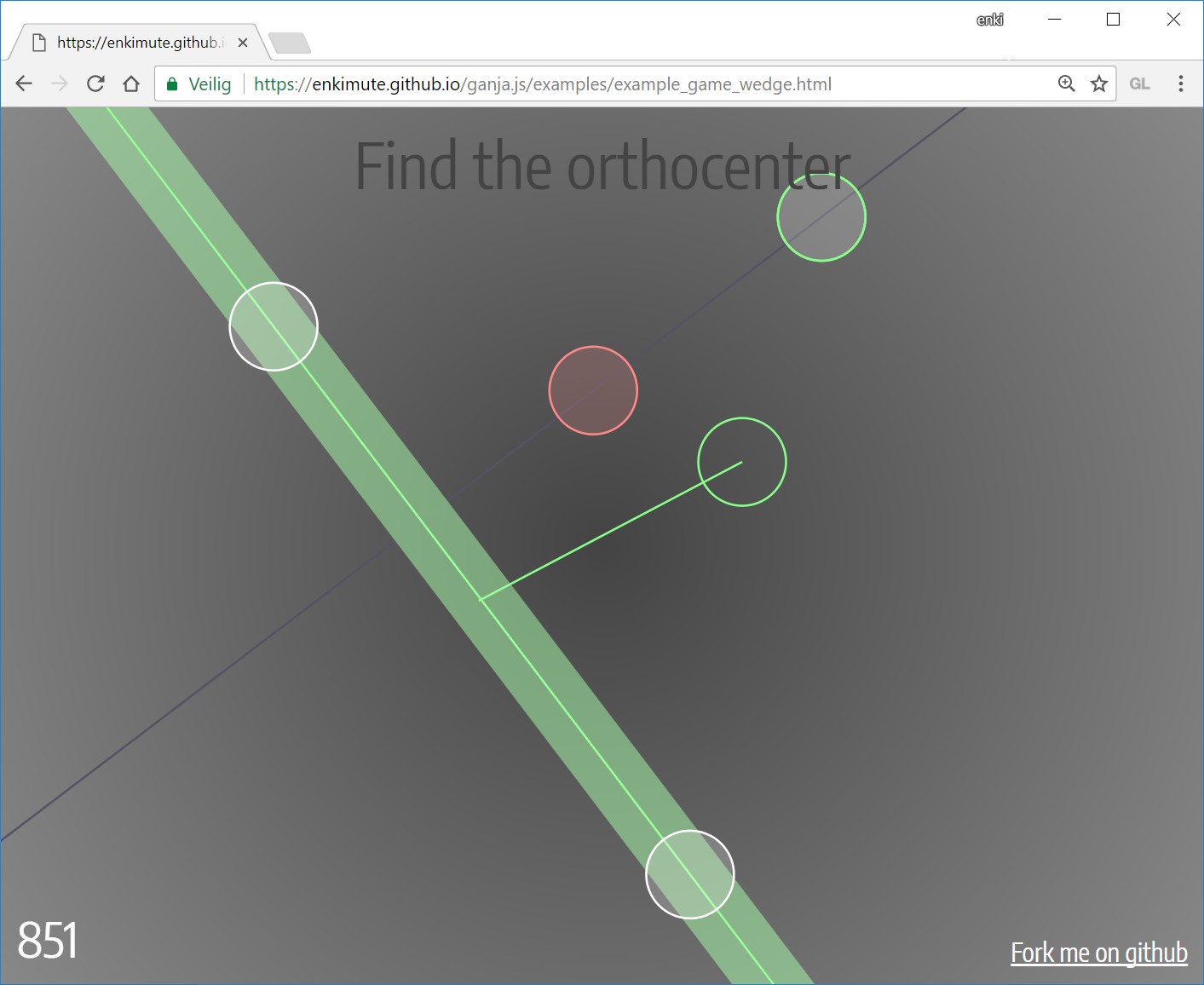
Or - get some hands on experience with euclidian plane PGA by playing the wedge game.
Ganja.js allows you to further customise the algebra class it generates, allowing you to generate subalgebras (who's elements use less storage), or algebra's where you decide on the order and name of the basis blades. (the name should always be exyz but you can pick e.g. e20 instead of the default e02 and expect ganja.js to make appropriate sign changes)
The advanced options are available by passing in an options object as the first parameter to the Algebra call.
// The complex numbers as the even subalgebra of R2
C = Algebra({p:2,basis:['1','e12']});
// The Quaternions as the even subalgebra of R3
var H = Algebra({p:3,basis:['1','e12','e13','e23']}); When not specified, ganja.js will generate basis names that are grouped by rank and numerically sorted. By default, a single zero dimension will get generator name e0. Zero dimensions come first.
| signature | default basis names |
|---|---|
| 2,0,0 and 1,1,0 | 1,e1,e2,e12 |
| 1,0,1 | 1,e0,e1,e01 |
| 3,0,0 and 2,1,0 | 1,e1,e2,e3,e12,e13,e23,e123 |
| 2,0,1 | 1,e0,e1,e2,e01,e02,e12,e012 |
| 4,0,0 and 3,1,0 | 1,e1,e2,e3,e4,e12,e13,e14,e23,e24,e34,e123,e124,e134,e234,e1234 |
| 3,0,1 | 1,e0,e1,e2,e3,e01,e02,e03,e12,e13,e23,e012,e013,e023,e123,e0123 |
note the scalar part of a multivector "mv" can be addressed with "mv.s", other basis blades follow the expected pattern. e.g. "mv.e12" or "mv.e012".
By default, your algebra elements will inherit from Float32Array. You can change the underlying datatype used by ganja.js to any of the typed array basis types :
var R3_32 = Algebra(3);
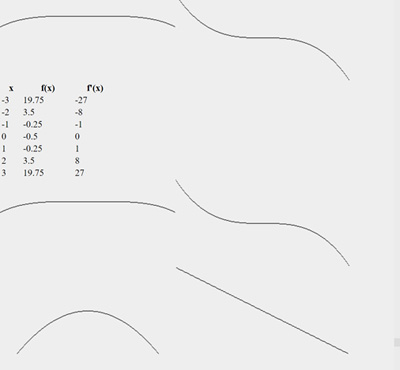
var R3_64 = Algebra({p:3,baseType:Float64Array});Or take things a bit further and simply specify a Cayley table to your liking. The example below shows automatic numerical differentiation and calculates the value, 1st, 2nd and 3rd derivative of any polynomial.
var basis=['1','e1','e2','e3'];
var Cayley=[['1', 'e1','e2','e3'],
['e1','e2','e3', '0'],
['e2','e3', '0', '0'],
['e3', '0', '0', '0']];
Algebra({basis,Cayley},()=>{
var f = (x)=>0.25*x*x*x*x-0.5;
for (var i=-5; i<5; i++) console.log( i, f(i+1e1) );
});outputs : x [f(x),f'(x),f''(x)/2!,f'''(x)/3!]
-5 [155.75, -125, 37.5, -5]
-4 [ 63.5, -64, 24, -4]
-3 [ 19.75, -27, 13.5, -3]
-2 [ 3.5, -8, 6, -2]
-1 [ -0.25, -1, 1.5, -1]
0 [ -0.5, 0, 0, 0]
1 [ -0.25, 1, 1.5, 1]
2 [ 3.5, 8, 6, 2]
3 [ 19.75, 27, 13.5, 3]
4 [ 63.5, 64, 24, 4]
For storage and performance reasons it can be interesting to combine elements of various sub-algebras of a given Algebra. Ganja.js supports this by setting options.mix to true when you create your algebra.
// Create R2 - Clifford algebra of 2D vectors - indicate you want mix mode.
var R2 = Algebra({p:2,q:0,r:0,mix:true});
// Create the complex numbers as the even subalgebra of R2.
var C = Algebra({p:2,q:0,r:0,basis:['1','e12'],mix:true});
// Elements of R2 have four components.
// Create the complex number 1+4i
var a=new R2([1,0,0,4])
// Elements of C have two components.
// Create the complex number 3+2i
var b=new C([3,2]);
// They inter-operate ..
a.Mul(b); // returns an element of R2 : [-5,0,0,14]
b.Mul(a); // returns an element of C : [-5,14]With the mix mode enabled, all operations generated by ganja.js will use basis name access instead of array indexing. (and all operations are protected to substitute missing blades with 0).
The Inline syntax can still be used, keep in mind that in most cases you would want that to be the inline function of the 'parent' algebra. (In the example above, use R2.Inline and not C.Inline as the latter will reduce all your operations to the field of C).
Here's a list of the supported operators in all syntax flavors :
Please note that operator precedence is as always in javaScript, except for Wedge, Vee, Dot and Sandwich which have higher precedence than * and /, resulting in less brackets in many common GA expressions.
| Precedence | Inline JS | AsciiMath | Object Oriented | Functional |
|---|---|---|---|---|
| 5 | x.Involute | tilde(x) | x.Involute | A.Involute(x) |
| 5 | x.Reverse | ddot(x) | x.Reverse | A.Reverse(x) |
| 5 | ~x | hat(x) | x.Conjugate | A.Conjugate(x) |
| 5 | !x | bar(x) | x.Dual | A.Dual(x) |
| 4 rtl | x**-1 | x^-1 | x.Inverse | A.Inverse(x) |
| 4 rtl | x**y | x^y | x.Pow(y) | A.Pow(x,y) |
| 3 | x^y | x^^y | x.Wedge(y) | A.Wedge(x,y) |
| 3 | x<<y | x*y | x.Dot(y) | A.Dot(x,y) |
| 3 | x&y | bar(bar(x)^^bar(y)) | x.Vee(y) | A.Vee(x,y) |
| 3 | x>>>y | x ** y ** hat(x) | x.Mul(y).Mul(x.Conjugate) | A.sw(x,y) |
| 2 | x*y | x**y | x.Mul(y) | A.Mul(x,y) |
| 2 | x/y | x/y | x.Div(y) | A.Div(x,y) |
| 1 | x-y | x-y | x.Sub(y) | A.Sub(x,y) |
| 1 | x+y | x+y | x.Add(y) | A.Add(x,y) |
| 1e1 | 1e_1 | new A([0,1]) | A.Vector(1) | |
| 2e2 | 2e_2 | new A([0,0,2,0]) | A.Vector(0,2) | |
| 2e12 | 2e_12 | new A([0,0,0,2]) | A.Bivector(2) |
The Duality operator implements Poincare duality, a definition and implementation that works even if the pseudoscalar of the subspace in consideration is degenerate. It is defined for any k-vector x of an n-dimensional subspace as the n-k vector y containing all the basis vectors that are not in x. For non-degenerate metrics, you can still use multiplication with the pseudoscalar if so desired (although it will be less efficient)
The dot product implemented is the left contraction - without any extensions or modifications. The geometric meaning is usually formulated as the dot product between x and y gives the orthogonal complement in y of the projection of x onto y.
The vee product is available as an optimized shorthand for the dual of the wedge of the duals.
a&b = !(!a^!b)
I've chosen the & symbol as it can be interpreted as 'join' or 'meet' depending on the geometric meaning given to vectors. (planes/lines or points)
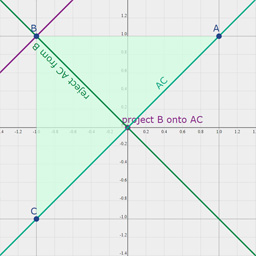
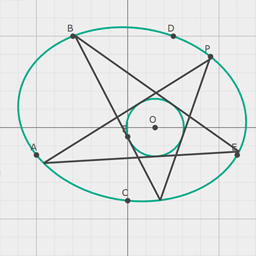
Want to get started quickly with 2D Projective Geometric Algebra ? The boiler plate below gets you going with a bunch of usefull identities. (and the coffeeshop has plenty of examples).
We start off with a clifford algebra with signature (2,0,1). We then upgrade it to a geometric algebra by extending it with geometric operators. (this is where we decide our bivectors will be points, effectively making this P(R*2,0,1).
Simply include the ganja.js script and put the block below in a SCRIPT tag to get started ..
// Create a Clifford Algebra with 2 positive and one zero generator.
Algebra(2,0,1,()=>{
// Output algebra info to the console.
this.describe();
// The default basis is s,e0,e1,e2,e01,e02,e12,e012
// The metric for vectors is 0, 1, 1 - Vectors will represent lines.
// The metric for bivectors is 0, 0, -1 - Bivectors will represent points.
// The pseudoscalar is degenerate, so use the built-in duality operator instead.
// The bivectors consist of two motor elements and one rotation element -
// exactly what is needed to represent translations and rotations in the plane.
// In dual projectivized space, the origin is represented by the e12 bivector.
var origin = 1e12, EX=-1e02, EY=1e01;
// Points and lines can be specified directly. (note : -e02 = e20)
var point = (x,y)=>origin+x*EX+y*EY;
var line = (a,b,c)=>a*1e1+b*1e2+c*1e0;
// Or through join and meet operations. (dual so wedge is meet and vee is join.)
var join = (p1,p2)=>p1&p2;
var meet = (l1,l2)=>l1^l2;
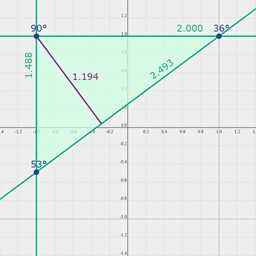
// Distances and angles
var dist_points = (P1,P2)=>(P1.Normalized&P2.Normalized).Length;
var dist_point_line = (P,l)=>((P.Normalized)^(l.Normalized)).e012;
var angle_lines = (l1,l2)=>(l1.Normalized<<l2.Normalized).s;
// Points and lines can be projected and rejected.
var project = (P,l)=>P<<l*l;
var parallel = (P,l)=>P<<l*P;
var ortho = (P,l)=>P<<l;
// translations and rotations.
var rotor = (a,P)=>Math.cos(a*0.5)+Math.sin(a*0.5)*P;
var translator = (x,y)=>1+0.5*(x*1e02-y*1e01);
// To demonstrate graphing, we create some points and lines.
// Users can drag points in the graph, lambda expressions can be
// used to create dynamic updating items.
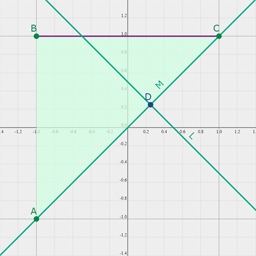
var A = point(-1,-1), B = point(1,-1), C = point(-1,1), l = line(-1,1,0.5);
// Ganja.js can directly graph 2D PGA elements. Pass in an array of
// items to render. (numbers are colors, strings are labels, PGA points
// and lines are rendered automatically and arrays can be used for line
// segments and polygons). The graph function returns a HTML SVG element.
document.body.appendChild(this.graph([
// use numbers to set the current color.
0x444444,
// strings label the items they follow, first string is a title.
"title",
// render points (user can drag these)
A, B, C, "Label for point",
// render lines
l,"Label for line",
// line segments
()=>[A,B], "Label for segment",
// polygons
0xffeeee,
()=>[A,B,C], 0xff7777, "Label for polygon"
],{grid:true, animate:false}));
// When using the animation mode, all lambda's will be evaluated every frame.
// Use Date.now() or similar. (many examples in the coffeeshop.)
});
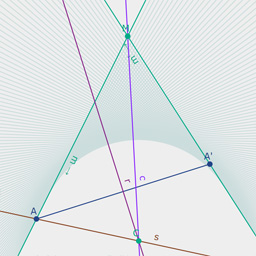
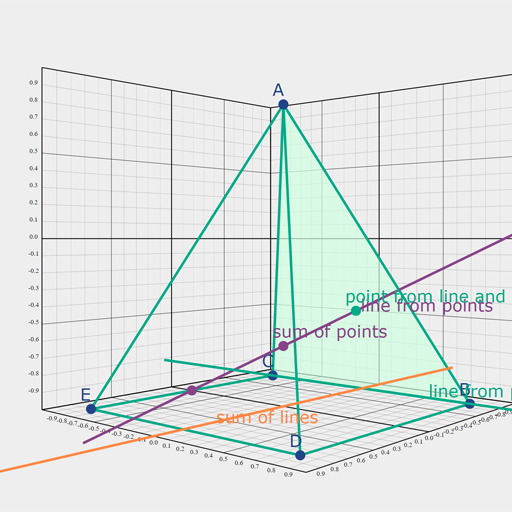
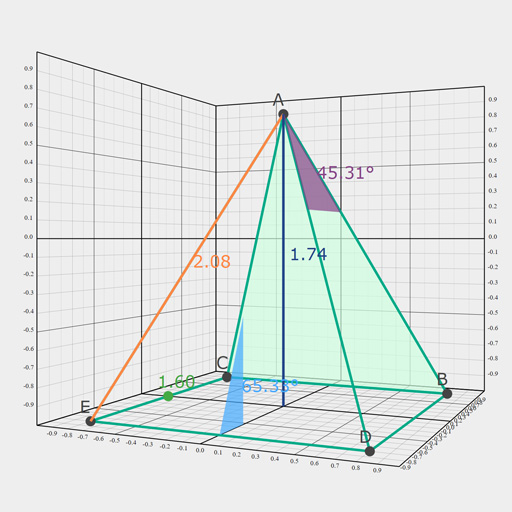
This example implements the table on page 15 of Gunn's Geometric Algebra for Computer Graphics. We apply the same strategy from above and start from a Clifford Algebra in R3,0,1.
// Create a Clifford Algebra with 3 positive and one zero generator.
Algebra(3,0,1,()=>{
// Output algebra info to the console.
this.describe();
// The default basis is 1,e0,e1,e2,e3,e01,e02,e03,e12,e13,e23,e012,e013,e023,e123,e0123
// The metric for vectors is 0, 1, 1, 1 - Vectors will represent planes.
// The metric for bivectors is 0, 0, 0, -1, -1, -1 - Bivectors will represent lines.
// The metric for trivectors is 0, 0, 0, -1 - Trivectors will represent points.
// The pseudoscalar is degenerate, so use the built-in duality operator instead.
// The bivectors consist of three motor elements and three rotation element -
// exactly what is needed to represent translations and rotations in euclidean space.
// In dual projectivized space, the origin is represented by the e12 bivector.
var origin=1e123, EX=-1e023, EY=1e013, EZ=-1e012;
// Points and planes can be specified directly.
var point = (x,y,z)=>origin+x*EX+y*EY+z*EZ,
plane = (a,b,c,d)=>a*1e1+b*1e2+c*1e3+d*1e0;
// Table from "Geometric Algebra for Computer Graphics" p.15
var LineFromPoints = (P,Q)=>P&Q,
LineFromPlanes = (a,b)=>a^b,
PointFromPlanes = (a,b,c)=>a^b^c,
PlaneFromPoints = (P,Q,R)=>P&Q&R,
DistPointToPlane = (a,P)=>a&P,
DistPoints = (P,Q)=>(P&Q).Length,
AnglePlanes = (a,b)=>Math.acos((a<<b).Length),
LineThroughPointPerpPlane = (P,a)=>P<<a,
OrthProjPointToPlane = (P,a)=>P<<a*a,
PlaneThroughPointParPlane = (P,a)=>P<<a*P,
IntersectLinePlane = (PI,a)=>PI^a,
PlaneThroughPointPerpLine = (PI,P)=>P<<PI,
OrthProjPointToLine = (PI,P)=>P<<PI*PI,
LineThroughPointParLine = (PI,P)=>P<<PI*P,
LineThroughPointPerpLine = (PI,P)=>(P<<PI*P)&P,
DistLines = (PI,EP)=>PI&EP,
AngleLines = (PI,EP)=>Math.acos((PI<<EP).Length),
ReflectionInPlane = (a,X)=>a*X*a,
Rotor = (PI,alpha)=>Math.cos(alpha/2) + Math.sin(alpha/2)*PI,
RotationAroundLine = (X,PI,alpha)=>Rotor(PI,alpha)*X*~Rotor(PI,alpha),
Translator = (x,y,z)=>1+0.5*(x*EX+y*EY+z*EZ);
// To demonstrate graphing, we create some points and lines.
// Users can drag points in the graph, lambda expressions can be
// used to create dynamic updating items.
var A = point(-1,-1, 0), B = point(1,-1, 0), C = point(-1,1,0);
// Ganja.js can directly graph 3D PGA elements. Pass in an array of
// items to render. (numbers are colors, strings are labels, PGA points
// and lines are rendered automatically and arrays can be used for line
// segments and polygons). The graph function returns a HTML SVG element.
document.body.appendChild(this.graph([
// use numbers to set the current color.
0x444444,
// strings label the items they follow, first string is a title.
"title",
// render points (user can drag these)
A, B, C, "Label for point",
// render lines
()=>(B&C&A)<<(B&C)<<-A,"Label for line",
// line segments
()=>[A,B], "Label for segment",
// polygons
0xffeeee,
()=>[A,B,C], 0xff7777, "Label for polygon"
],{grid:false, animate:false}));
// When using the animation mode, all lambda's will be evaluated every frame.
// Use Date.now() or similar. (many examples in the coffeeshop.)
});