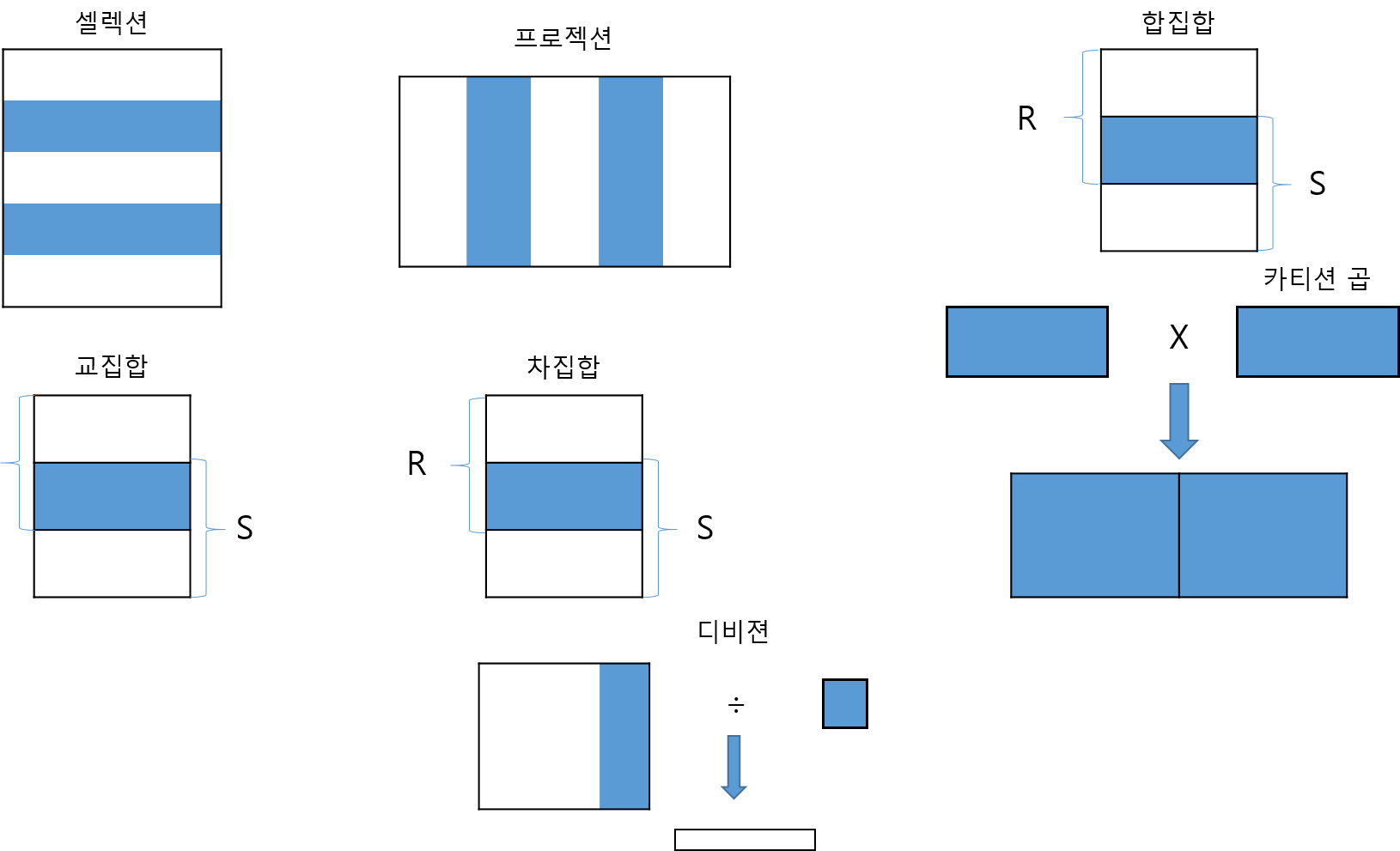
관계해석(relational calculus)은 원하는 데이터만 명시하고 질의를 어떻게 수행할 것인지는 명시하지않는 선언적인 언어, 관계대수(relational algebra)는 어떻게 질의를 수행할 것인가를 명시하는 절차적 언어.
: 한 릴레이션에서 selection 조건(=predicate)을 만족하는 투플들의 부분 집합을 생성한다. 즉, 주어진 조건을 만족하는 투플들만 걸러내는 연산으로 생각할 수 있다.
- 단항 연산자(하나의 입력 릴레이션에 적용)
- 결과릴레이션의 차수는 입력릴레이션의 차수와 같다.
- {=,<>,<=,<,>=,>}
- {AND,OR,NOT}
<애트리뷰트> 비교연산자 <상수> <애트리뷰트> 비교연산자 <애트리뷰트> <조건> AND/OR <조건> NOT <조건>
: 한 릴레이션의 애트리뷰트들의 부분집합.
- 새로운 릴레이션의 차수는 애트리뷰트 리스트내의 애트리뷰트와 같다.
- 프로젝션 연산의 결과 릴레이션에는 입력릴레이션으로부터 골라낸 일부 애트리뷰트만 포함되므로 중복된 투플들이 존재할 수 있다.
- 키가 포함되어있으면 중복이 존재하지 않는다.
: 릴레이션이 투플들의 집합이기 때문에 기존의 집합 연산이 릴레이션에 적용된다.
- 합집합 호환(union compatible) R1(A1,A2,...,An),R2(B1,B2,...,Bm)이 합잡합 호환일 필요충분조건은 n=m이고, 모든 1<=i<=n에 대해 domain(Ai)=domain(Bi)이다. 즉, 두릴레이션의 애트리뷰트 수가 같고 대응되는 도메인이 같은것.
R∪S, R 과 S 두 릴레이션의 합집합 연산 결과 릴레이션의 차수는 R or S의 차수와 같으며,결과 릴레이션의 애트리뷰트 이름들은 R or S의 애트리뷰트들의 이름과 같다.
R∩S,R 과 S 두 릴레이션의 교집합 연산 결과 릴레이션의 차수는 R or S의 차수와 같으며,결과 릴레이션의 애트리뷰트 이름들은 R or S의 애트리뷰트들의 이름과 같다.
R-S,R 과 S 두 릴레이션의 합집합 연산 결과 릴레이션의 차수는 R or S의 차수와 같으며,결과 릴레이션의 애트리뷰트 이름들은 R or S의 애트리뷰트들의 이름과 같다.
:한 릴레이션의 투플들을 다른 릴레이션의 투플들과 연관시키기 위해서 흔히 두 릴레이션의 투플들을 결합해야하는 경우가 있다. R X S의 차수는 n+m이고, 카디날리티는 i*j이고, 애트리뷰트(A1,..,An,B1,...Bm)이다. 카티션곱의 결과 릴레이션의 크기가 매우 클 수 있고, 원하는 결과는 일부분인 경우가 대부분이므로 유용한 연산자는 아니다
: 두 개의 릴레이션으로 부터 연관된 투플들을 결합하는 연산자. (두 개 이상의 릴레이션 관계를 다룰 때 매우 중요)
R과 S의 세타조인의 결과는 차수는 n+m이고, 애트리뷰트(A1,..,An,B1,...Bm)이며, 조인조건을 만족하는 투플로 이루어진 릴레이션이다. 세타는 **{=,<>,<=,<,>=,>}**중의 하나이다. 동등 조인은 세타조인 중에서 비교연산자가 **=**인 조인.
동등조인의 결과는 R과 S의 카티션 곱에 실렉션을 적용한 것과 같다.
동등 조인의 결과 릴레이션에서 조인 애트리뷰트를 한개 제외한 것. 가장 많이 사용된다.
R(A1,...An,B1,..,Bm), S(B1,..,Bm)인 두릴레이션의 R÷S는 차수가 n이고, S에 속하는 모든 투플에 대해 R에 존재하는 투플들의 집합.
- 산술 연산을 할 수 없다.
- 집단 함수를 지원하지 않는다.
- 정렬을 나타낼 수 없다.
- 데이터베이스를 수정할 수없다.
- 중복된 투플을 나타내는 것이 필요할 때가 있는데 이를 명시하지 못한다.
: 상대 릴레이션에서 대응되는 투플을 갖지 못하는 투플이나 조인 애트리뷰트에 널값이 들어있는 투플들을 다루기 위해서 확장한것. 두 릴레이션에 대응되는 투플들을 결합하면서 , 대응되는 투플을 갖지 않는 투플과 조인 애트리뷰트에 널값을 갖는 투플도 포함.