BST는 다음과 같은 속성을 만족시키는 이진 트리이다.
- 각 노드에 값이 있다.
- 값이 중복된 노드가 없다.
- 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
- 노드의 오른쪽 서브트리에는 그 노드의 값과 같거나 큰 값들을 지닌 노드들로 이루어져 있다.
- 좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.
이진탐색트리를 inorder traversal 방식을 씁니다. 이렇게 하면 이진탐색트리 내에 있는 모든 값들을 정렬된 순서대로 읽을 수 있습니다.
- 이진 탐색 트리에서 Key 값 x를 가진 노드를 검색하고자 할 때, 트리에 해당 노드가 존재하면 해당 노드를 리턴하고, 존재하지 않으면 NULL 리턴
- 검색하고자 하는 값을 루트노드와 먼저 비교해 일치할 경우 루트노드 리턴
- 불일치하고 검색하고자 하는 값이 루트노드의 값보다 작을 경우 왼쪽 서브트리에서 재귀적 검색
- 불일치 하고 검색하고자 하는 값이 루트 노드의 값과 같거나 큰 경우 오른쪽 서브트리에서 재귀적 검색
Node * search(Node * root, int key){
if(root==NULL||root->key == key) return root;
if(key<root->key)return search(root->left, key);
else return search(root->right, key);
}- 삽입을 하기 전에 검색을 수행한다.
- 트리를 검색한 후 키와 일치하는 노드가 없으면 마지막 노드에서 키와 노드의 크기를 비교하여 왼쪽이나 오른쪽에 새로운 노드를 삽입한다.
Node * insert(Node * node,int key){
if(node == NULL) return new_node(key);
if(node->key>key)node->left=insert(node->left,key);
else node->right=insert(node->right,key);
return node;
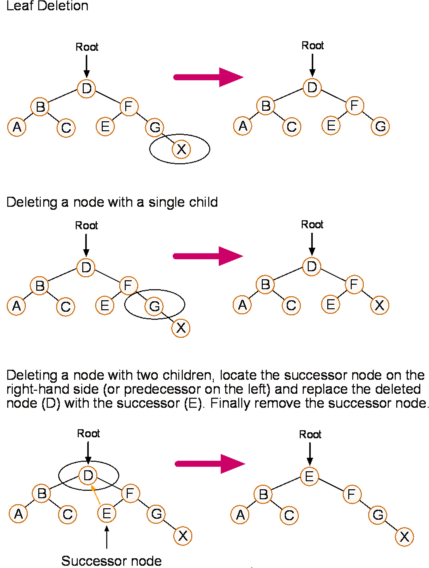
}삭제하려는 노드의 자식 수에 따라서
- 단말노드 삭제 : 해당 노드를 단순히 삭제한다.
- 자식노드가 1개인 노드 삭제 : 해당 노드를 삭제하고 그 위치에 해당 노드의 자식노드를 대입한다.
- 자식노드가 2개인 노드 삭제 : 삭제하고자 하는 노드의 값을 해당 노드의 왼쪽 서브트리에서 가장 큰값으로 대체하거나, 오른쪽 서브트리에서 가장 작은 값으로 대체한 뒤, 해당 노드(왼쪽서브트리에서 가장 큰 값을 가지는 노드 또는 오른쪽 서브트리에서 가장 작은 값을 가지는 노드)를 삭제한다.
Node * min(Node * node){
Node * p = node;
// 가장 왼쪽 단말 노드로 이동
while (p->left != NULL)
p = p->left;
return p;
}
Node * delete(Node * root, int key){
Node * tmp = NULL;
if (root == NULL) return root; // 순환 멈춰주는 부분(basecase)
if (key < root->key)
root->left = delete(root->left, key);
else if (key > root->key)
root->right = delete(root->right, key);
else // key == root->key
{
// 1. 오른쪽 자식 노드가 있을 때
if (root->left == NULL){
tmp = root->right;
free(root);
return tmp;
}else if (root->right == NULL){
//2. 왼쪽 자식 노드가 있을 때
tmp = root->left;
free(root);
return tmp;
}
// 자식노드가 두개 일때
tmp = min(root->right);
// 루트 키 값을 변경해주고
root->key = tmp->key;
// key값을 찾아서 삭제한다.
root->right = delete(root->right, tmp->key);
}
return root;
}