정렬이란 물건을 크기 순으로 오름차순이나 내림차순으로 나열한 것이다.
- 단순하지만 비효율적 : 삽입, 선택, 버블 정렬
- 복잡하지만 효율적 : 퀵, 히프, 합병, 기수 정렬
- 주어진 리스트 중에 최솟값을 찾는다.
- 그 값을 맨 앞에 위치한 값과 교체한다(패스(pass)).
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
비교하는 것이 상수 시간에 이루어진다는 가정 아래, n개의 주어진 리스트를 이와 같은 방법으로 정렬하는 데에는 O(n^2) 만큼의 시간이 걸린다.
void selection_sort(int list[], int n){
int i, j, least,tmp;
for(i=0;i<n-1;i++){
least = i;
for(j=i+1;j<n;j++){
if(list[j]<list[least]){
least = j;
}
SWAP(list[i],list[j],tmp);
}
}
}자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다.
void insert_sort(int arr[],int n){
int i, key, j;
for (i = 1; i < n; i++)
{
key = arr[i];
j = i-1;
while (j >= 0 && arr[j] > key)
{
arr[j+1] = arr[j];
j = j-1;
}
arr[j+1] = key;
}
}- 복잡도
- 최선의 경우(이미 정렬) : O(n)
- 최악의 경우(역순으로 정렬된 경우) : O(n^2)
인점한 2개의 레코드를 비교하여 순서대로 되어 있지 않으면 서로 교환한다.
void bubble_sort(int list[], int n){
int i,j,tmp;
for(i=n-1;i>0;i--){
for(j=0;j<i;j++){
if(list[i]<list[j])SWAP(list[i], list[j], tmp);
}
}
}- 복잡도(최상, 평균, 최악) : O(n^2)
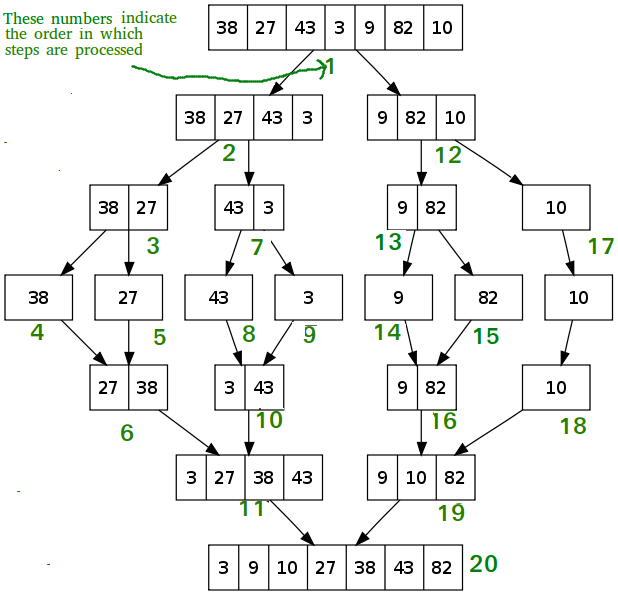
- 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분리시트를 정렬한다.
- 정렬된 두개의 부분 리스트를 합하여 전체 리스트를 정렬한다.
void merge(int array[], int left, int mid, int right)
{
int i, j, k, m;
i = left;
j = mid + 1;
k = left; //결과 배열의 인덱스
int tempArray[MAX];
//left부터 mid 까지의 블록과 mid+1부터 right까지의 블록을 서로 비교하는 부분
while (i <= mid && j <= right) {
if (array[i] < array[j]){ //left index 값이 right index 값보다 작으면 left index 값을 결과 result에 복사
tempArray[k] = array[i];
i++;
}else{ //아니라면 right index 값을 결과 result에 복사
tempArray[k] = array[j];
j++;
}
k++;
}
// left 블록의 값은 다 처리되었는데 right 블록의 index가 아직 남아있을 경우
// right index를 순차적으로 결과 result에 복사
if (i > mid){
for (m = j; m <= right; m++){
tempArray[k] = array[m];
k++;
}
} else { // left 블록의 index가 아직 남아있을 경우 left index를 순차적으로 결과 result에 복사
for (m = i; m <= mid; m++){
tempArray[k] = array[m];
k++;
}
}
for(m = left; m <= right; m++){
array[m] = tempArray[m];
}
}
void merge_sort(int array[], int left, int right)
{
int mid;
// 분할이 다 되지 않았을 경우 if 문 실행
if(left < right){
mid = (left + right)/2;
merge_sort(array, left, mid); //왼쪽 블록 분할
merge_sort(array, mid+1, right); //오른쪽 블록 분할
merge(array, left, mid, right); //분할된 블록 병합
}
}- 복잡도 : O(n*log(n))
기수 정렬은 정수의 자리수를 기준으로 낮은 자리수부터 비교해 정렬하는 알고리즘입니다.
예를 들어 3자리 수라면 1의자리, 10의자리 , 100의 자리 숫자를 순서대로 비교해서 정렬하는 방법입니다.
void radix_sort(int a[])
{
int i, b[MAX], m=0, exp=1;
// m에 최대값을 저장
for( i=0 ; i<MAX ; i++ )
{
if( a[i] > m )
m = a[i];
}
// m의 자리수보다 exp가 커지면 종료
while( m/exp > 0 )
{
int bucket[10] = {0}; //수별로 비교해서 임시로 저장해둘 공간
for( i=0 ; i<MAX ; i++ )
bucket[a[i]/exp%10]++;
for( i=1 ; i<10 ; i++ )
bucket[i] += bucket[i-1];
for( i=MAX-1 ; i>=0 ; i-- )
b[--bucket[a[i]/exp%10]] = a[i];
for( i=0 ; i<MAX ; i++ )
a[i] = b[i];
exp *= 10; //자리수 비교가 끝나면 다음 자리수!
}
}- 복잡도 : O(dn) d는 자릿수
- pivot(기준값) 정하기
- pivot보다 작은 원소들은 왼쪽, 큰 원소는 오른쪽
- pivot을 기준으로 왼쪽 배열과 오른쪽 배열을 새로운 배열로 정하고 각 배열구간에서 1번과정 재귀적 반복
- 일반적으로 처음 또는 마지막 원소를 pivot으로 잡는다.
int partition (int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high- 1; j++)
{
if (arr[j] <= pivot)
{
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
//pi = partition index
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}#include <algorithm>
bool compare(int a, int b){
// 오름차순
// return a<b;
// 내림차순
return a>b;
}
bool comparep(POINT a, POINT b){
if(a.x == b.x ) return a.y < b.y;
else return a.x < b.x;
}
//처음부터 n-1번째까지 원소를 compare함수의 정의대로 정렬
//퀵정렬 기반으로 정렬한다.
//std::sort(정렬할 자료의 시작 주소, 정렬할 자료의 마지막 주소,[비교함수 주소])
std::sort(S,S+n,compare);- 복잡도 O(nlog(n))
힙 정렬(heap sort)
- n개의 노드에 대한 완전이진트리를 구성한다. 이때 루트 노드부터 부노드, 왼쪽 자노드, 오른쪽 자노드 순으로 구성한다.
- 최대 힙을 구성한다.
- 한번에 하나씩 요소를 힙에서 삭제하면서 저장한다.
힙 정렬이 최대로 유용한 경우는 전체 자료가 아닌 가장 큰 값 몇개만 필요할 때이다.
- 힙구현은 힙(heap)에서 확인할 수 있다.
void heap_sort(int arr[], int n){
int i;
Heap heap;
init(&heap);
for(i=0;i<n;i++){
insert_max(&heap, arr[i]);
}
for(i=n-1;i>=0;i--){
arr[i]=delete_max(&heap);
}
}- 복잡도
- 힙 삭제 시간 O(logn)*n = O(nlogn)