类
构造函数
+类
构造函数
+什么情况下会合成构造函数?
-
+
- 如果一个类没有任何构造函数,但他含有一个成员对象,该成员对象含有默认构造函数,那么编译器就为该类合成一个默认构造函数,因为不合成一个默认构造函数那么该成员对象的构造函数不能调用; +
- ,没有任何构造函数的类派生自一个带有默认构造函数的基类,那么需要为该派生类合成一个构造函数,只有这样基类的构造函数才能被调用; +
- 带有虚函数的类,虚函数的引入需要进入虚表,指向虚表的指针,该指针是在构造函数中初始化的,所以没有构造函数的话该指针无法被初始化; +
- 带有一个虚基类的类 +
并不是任何没有构造函数的类都会合成一个构造函数
编译器合成出来的构造函数并不会显示设定类内的每一个成员变量
拷贝构造函数
class A { A(const A & a);};
对象不存在,使用别的已存在的对象来初始化时会用到拷贝构造函数
+对象存在,则是用赋值运算符,因此赋值运算符需要在初始化对象前检查源对象和新建对象是否相同
+移动构造函数
+用a初始化b后,就把a析构,采用的是浅拷贝
为什么要用引用?
拷贝构造函数会在以下情况中被调用:1. 函数参数中作为值传递 2. 不作优化时,将类对象作为函数返回值 3. A = B,调用拷贝构造函数
当不使用引用而使用值传递时,拷贝构造函数本身又会调用自身,不断嵌套下去直到栈溢出
引用可以改成指针吗?
不可以,改成指针后会变成普通的有参构造函数
什么时候会生成默认拷贝构造函数?
当符合位拷贝语义时,无需生成默认拷贝构造函数,而是会直接调用构造函数
当不符合位拷贝语义时,才需要生成默认拷贝构造函数:1. 类有内部类对象,包含拷贝构造函数 2. 类继承于基类,基类有拷贝构造函数 3. 类中含有虚函数,需要有默认的拷贝构造函数来完成对虚函数指针的指向,否则Base base = thrive虚指针发生切割行为,4. 类存在虚继承,也会发生虚指针漂移,需要生成默认的拷贝构造函数
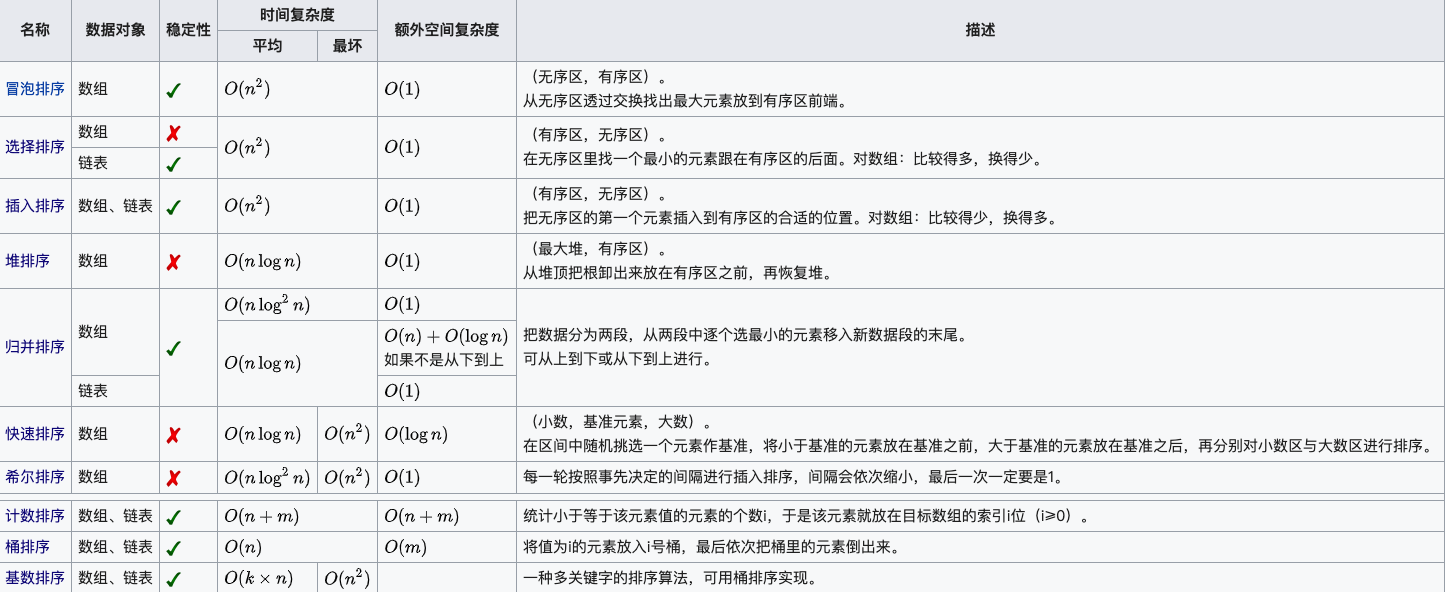
排序算法
冒泡排序
思路:遍历第 0 个元素到第 n - 1 个元素,比较第i个元素与第i+1个元素,每轮遍历都能将最小(大)元素放至头(尾),这个过程就像冒泡一样。
-1 | |
最快的情况是已有序,最慢的情况是逆序,平均时间复杂度是O(n2),是一种稳定的排序算法
-可优化的做法是通过flag判断是否已经有序,有序时则可早退
-选择排序
思路:每次遍历在未排序序列中选出最小(大)的数放置到已排序序列的末尾
-1 | |
时间复杂度为O(n2),选择排序并不稳定,如[3, 5, 5, 4],就会改变两个5的相对位置。适用于小型数据集排序
-插入排序
思路:分为未排序序列和已排序序列,将未排列序列逐一插入到已排序序列中的相应位置
-1 | |
时间复杂度为O(n2),不需要额外内存来存储中间结果,是稳定的排序算法
-希尔排序
也称递减增量排序,将序列分成更小的序列,然后对小序列使用插入排序,从而减小排序列表交换次数。非稳定排序
-首先定义一个增量序列的整数序列,用于确定子序列大小,最常用的增量序列是Knuth序列
-1 | |
以增量序列为步长,从最大增量开始,向下迭代到最小增量
-1 | |
归并排序
思路:基于分而治之的思想,将序列不断细分,细分成只有一个或两个元素的子序列,排序好后再合并回原来规模的序列。不需要交换比较,需要创建一个临时数组保存结果
-递归法
1 | |
优化1:用不同方法处理小规模问题,减少函数调用次数:在小数组上用插入排序,if(en - st <= 10){Insert_sort(vector<int>& nums, int st, int en);}
优化2:剪枝,在合并前先判断两个子序列是否已经有序,即nums[st] < ... < nums[mid] < ... < nums[en]
时间复杂度为O(nlogn),空间复杂度为O(n)
-迭代法
1 | |
时间复杂度是O(nlogn),避免了递归调用产生的栈空间消耗,适用于处理大规模数据,特别是可以通过并行化加快排序过程。归并排序是稳定排序
-快速排序
思路:选出一个元素称为基准元素,将所有比基准值小的移动到基准左边,比基准值大的移动到右边,最后递归地把两边的子序列排序
-1 | |
时间复杂度O(nlogn),就地排序,容易并行化
-堆排序
先创建一个堆,不断把堆首元素与堆尾互换,再调整堆,保证堆首的一直都是未排序的最大值,
-1 | |
堆排序的平均时间复杂度为 Ο(nlogn)
-计数排序
当输入的元素是 n 个 0 到 k 之间的整数时,它的运行时间是 Θ(n + k)。计数排序不是比较排序,排序的速度快于任何比较排序算法
-思路:找出待排序数组中的最大和最小元素,创建大小为 k=max−min+1的计数数组,记录数组中每个元素值出现次数,反向填充目标数组
-1 | |
时间复杂度:O(n+k),其中 n 是数组的长度,k 是元素的范围。空间复杂度:O(k+n),需要额外的计数数组和输出数组。
-从后向前遍历原数组,确保排序的稳定性,适用于元素范围较小的情况
-桶排序
桶排序是计数排序的改进版,利用函数映射关系与桶对应,而不是根据元素大小开辟数组
-思路:设定定量的数组当空桶,遍历序列一一放置到对应的桶中,对非空桶进行排序,最后放置回原数组
-1 | |
桶排序的平均时间复杂度是 O(n+k),其中 n 是元素个数,k 是桶的数量。如果元素均匀分布,排序时间为O(n),最坏情况下,所有元素落入一个桶中,时间复杂度退化为O(nlogn)
-基数排序
思路:将整数按位数切割成不同的数字,然后按每个位数分别比较
-1 | |

基于非比较的算法:计数排序、桶排序、基数排序
-就地排序算法:冒泡排序、选择排序、插入排序、对排序、希尔排序
-稳定排序算法:冒泡排序、插入排序、归并排序、基数排序
-非稳定排序算法:选择排序、快速排序、希尔排序、堆排序
-外部排序算法:归并排序、基数排序、堆排序、桶排序
+多态
多态是指指向派生类的基类指针在运行时,可以根据派生类对象类型来对不同虚函数进行调用。底层原理是当派生类对基类的虚函数进行重写时,派生类的虚表指针指向的是自身的虚表,而不是基类的虚表。(编译器自动为每个含有虚函数的类生成一份虚表)
+析构函数为什么要写成虚函数
由于类的多态性,可以有指向派生类的基类指针,这时如果删除基类指针,会调用指向的派生类对象的析构函数,派生类析构函数自动调用基类的析构函数,这样整个派生类对象完全被释放。如果析构函数不是虚函数,就会静态绑定到基类,删除基类指针时只会调用基类的析构函数,而导致内存泄露
+构造函数能声明为虚函数或纯虚函数吗?析构函数呢
构造函数不能声明为虚函数或纯虚函数,因为如果构造函数是虚函数,虚函数的调用通过虚指针和虚表,但虚表需要在类对象初始化后才有,无法找到调用所需的虚表
+一般情况下基类析构函数是虚函数,也可以是纯虚函数,含有纯虚函数的类是抽象类,不能被实例化
+虚表放在内存的什么区,虚指针初始化时间
虚函数表在类中共享,全局只有一个,在编译时构造完成。
+派生类在不重写基类虚函数时,虚表地址与基类不同,虚表中虚函数地址与基类中虚函数地址相同
+派生类在重写基类虚函数时,虚表地址与基类不同,虚表中虚函数地址也与基类中虚函数地址不同
+每个类对象的前四个字节保存虚指针,指向虚函数表。
+由于虚表的元素是虚函数的地址,不是程序代码,也就不会存储在代码段,并且类中的虚函数个数在编译期确定,不必动态分配,也就不会在堆区。所以虚表储存只读数据段,也就是常量区当中,虚函数则储存在代码段。C++内存模型有堆区、栈区、常量区、代码区和数据区(BSS未初始化段、已初始化段)
+构造函数、析构函数、虚函数可否声明为内联函数
构造函数和析构函数声明为内敛函数没有意义。
+虚函数只有当指向类本身的指针调用时,才会内联展开;当指向派生类的指针调用时(多态),并不会内联展开
+构造函数、析构函数可否抛出异常
构造函数可以抛出异常,当异常抛出,未完成的对象不会被创建,自动调用已构造对象的析构函数释放已分配资源。但因为析构函数不能被调用,可能会造成内存泄露
+析构函数不建议抛出异常,如果析构函数在另一个异常正在传播时,会导致程序异常终止
+因此,尽量避免手动管理资源, 使用RAII类进行封装。为了避免在析构函数中抛出异常,可以捕获并处理异常:在析构函数内部捕获所有可能的异常,避免将异常抛出;**使用 noexcept**:将析构函数声明为 noexcept(默认情况下,析构函数是 noexcept(true)),确保在析构过程中不会抛出异常
虚拟继承作用
虚继承是一种解决菱形继承问题的机制,确保在多重继承下,基类只被继承一次。最低层的派生类负责虚基类的构造