本章首先介绍搜索求解的概念、重要性、分类、应用场景;然后对搜索进行形式化描述;最后介绍两类搜索,即盲目搜索和启发式搜索,为后面介绍智能算法奠定基础。
- 人工智能经典三大基本技术为:知识表示、推理、搜索策略。
- 搜索定义:根据问题的实际情况寻找可用知识,并利用已知条件(知识),构造出一条代价较小的推理路线,寻求解决问题的办法的过程。
- 重要性:搜索直接关系到智能系统的性能与运行效率;搜索技术渗透在各种人工智能系统中。专家系统、自然语言理解、自动程序设计、模式识别、机器学习、信息检索和博弈等领域都广泛使用搜索技术。
- 博弈游戏(五字棋等)
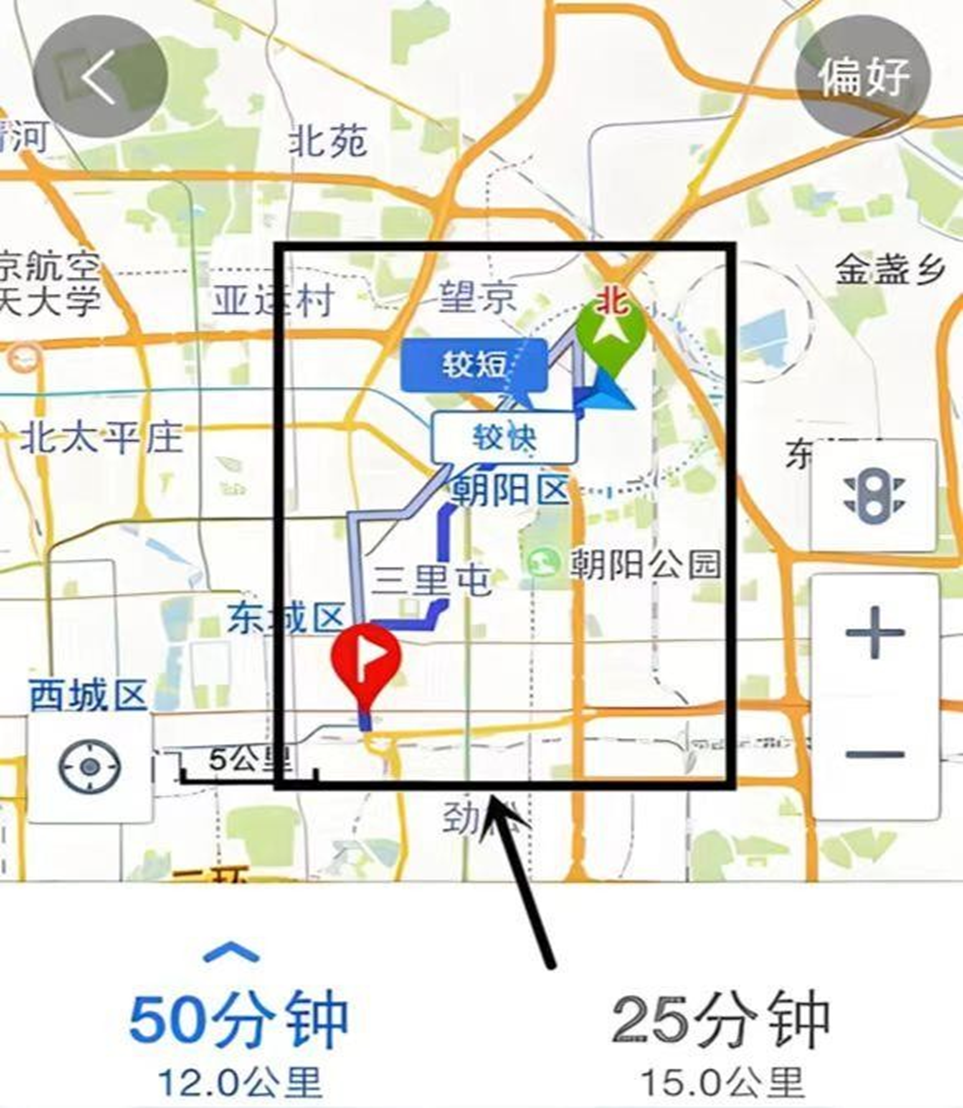
- 旅行路径规划问题
- 芯片布线问题
- 机器人导航问题
- 蛋白质设计问题
- …
京东物流亚洲一号(无人仓储)
- 无人仓:2018年5月24日,京东首次公开位于上海嘉定区的亚洲一号无人仓。物流机器人占地40000m2 ,主要由仓储和分拣两部分组成,仓内机器人包括AGV(自动分拣运输机)叉车、六轴机器人、自动供包机器人等不同工种。在分拣区,“小红人” 井然有序进行取货、扫码、运输、投货。依靠视觉识别和智能导航技术,“小红人”能以最优线路完成商品的拣选。
- 智慧大脑:而操控全局的智能控制系统是京东自主研发的“智慧”大脑,仓库管理、控制、分拣和配送信息系统等均由京东总集成。
- 降本增效:与传统的仓库相比,无人仓可以大幅度减轻工人的劳动强度,且效率是传统仓库的10倍。
当我们要设计一个通用AI,最需要(或者说唯一需要)考虑的是怎么让它有能力做出像人一样的决策。
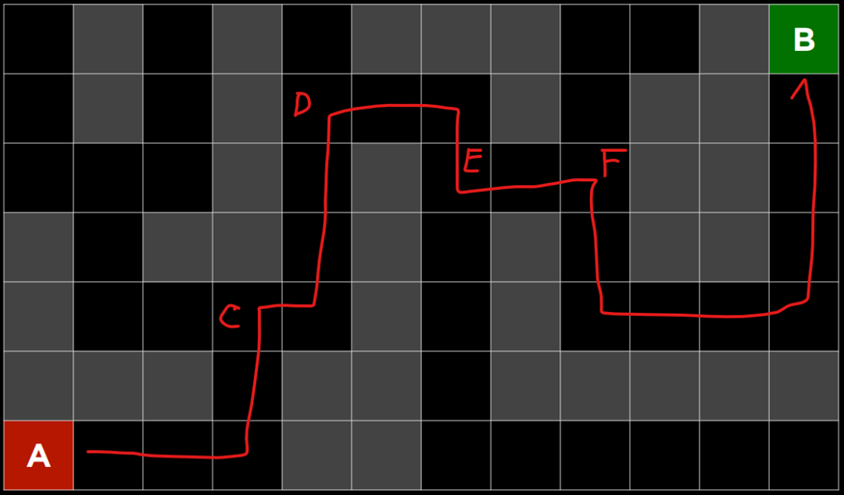
怎么从A走到B?(黑色可走,灰色不通)
如果是人看着地图来走,当然很简单,正常人都能迅速找到下面这条红色的路径来:
但是想一想,在C、D、E、F这几个点,明明还有其他选择,为什么你坚定选择了图上红线的方向呢?
显然,因为你一眼就看到了所有的可能路径,并且迅速在其中找到了最短的那条路。
复杂问题来了:如果是下面这张迷宫呢?靠人眼很难一眼就看出怎么走最好。
怎么办?你需要用笔去试探从A开始往B走的每个节点的所有可能,然后走到死路再去尝试其他可能,等最终找到了一条到B的通路,你也无法判断这条路是不是最短的路。
- 它要知道A和B在哪里。
- 它需要知道A和B之间所有的路况。(哪里是墙,哪里是路)
- 它需要知道在每一个有选择的路口,它应该往哪个方向走。
- 是否一定能找到一个解。
- 找到的解是否是最佳解。
- 时间与空间复杂度如何。
- 是否终止运行或是否会陷入一个死循环。
当我们要设计一个通用AI,最需要(或者说唯一需要)考虑的是怎么让它有能力做出像人一样的决策。
一个搜索问题可以用5个组成部分形式化描述。
问题的解:就是从初始状态到目标状态的一组行动序列。
最优解:所有解里面代价最小的解即为最优解。
- 状态空间:对智能体和环境当前情形的描述。(初始状态、目标状态)
- 动作:从当前时刻所处状态转移到下一时刻所处状态所进行操作。
- 状态转移:智能体选择了一个动作之后,其所处状态的相应变化。
- 路径/代价:一个完整的状态序列。该状态序列被一系列操作所连接。如一条完整的路径。
- 目标测试:评估当前状态是否为所求解的目标状态。
- S:状态集合。
- O:操作算子集合。
- S0:包含问题的初始状态,是S的非空子集。
- G:若干具体状态或满足某些性质的路径信息描述。
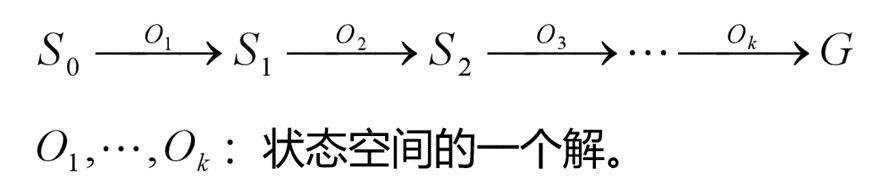
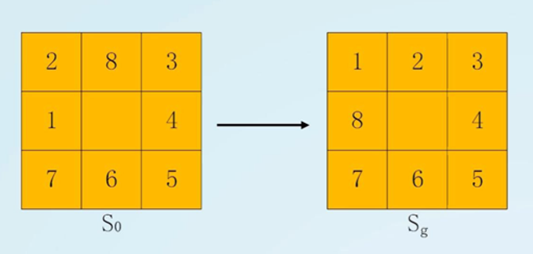
求解路径:从S0节点到G节点的路径。
状态空间解:一个有限的操作算子序列。
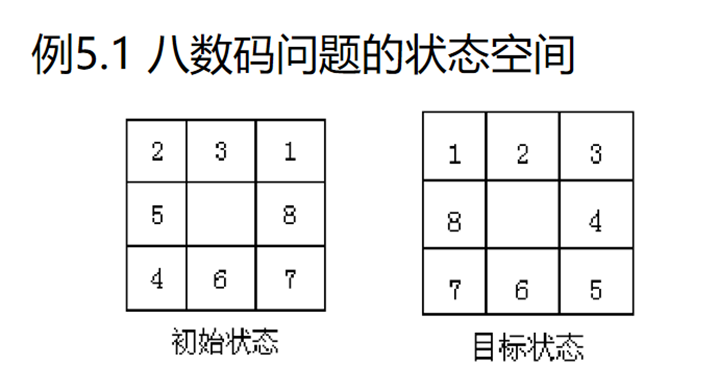
状态集S:所有的八数码摆法
操作算子集O: 将空格向上移动Up
将空格向下移动Down
将空格向左移动Left
将空格向右移动Right
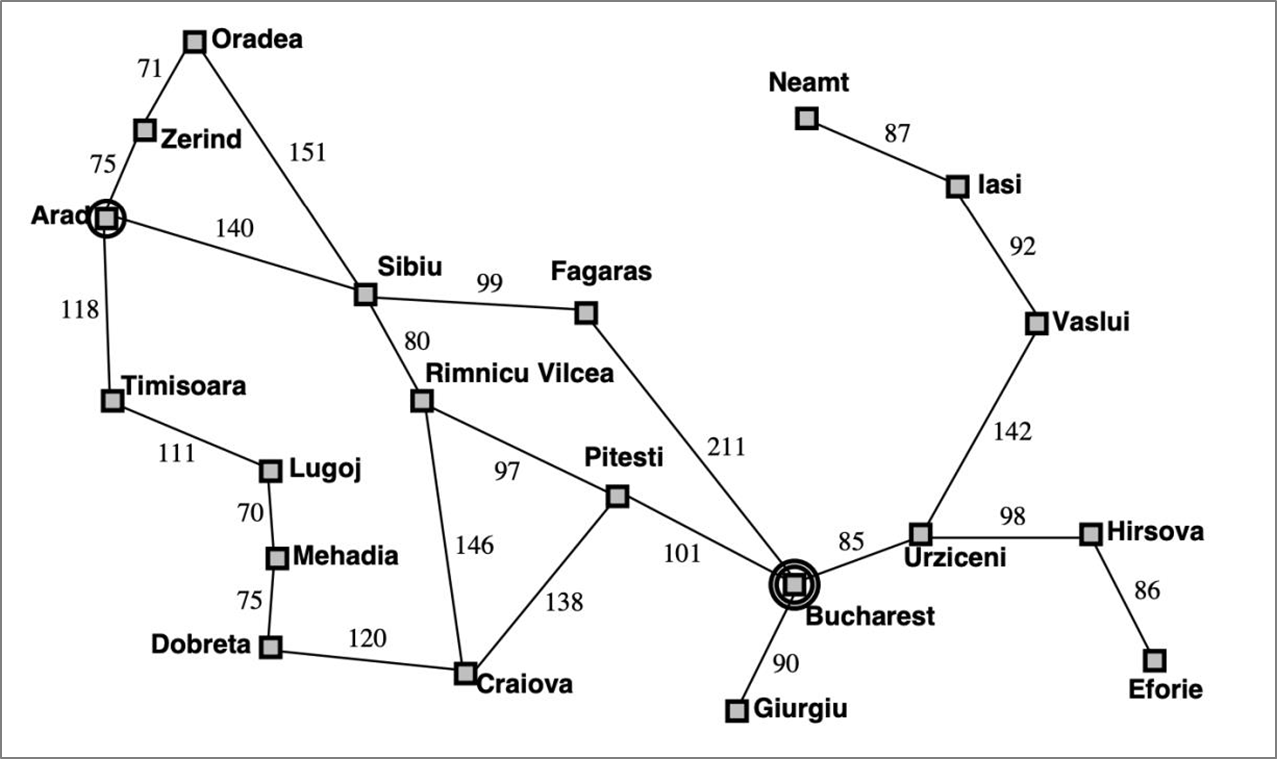
状态空间可用有向图来描述,图的节点表示问题的状态,图的弧表示状态之间的关系,即操作算子。
状态空间图对问题的求解就相当于在有向图上寻找一条从初始状态节点到目标状态节点的路径。
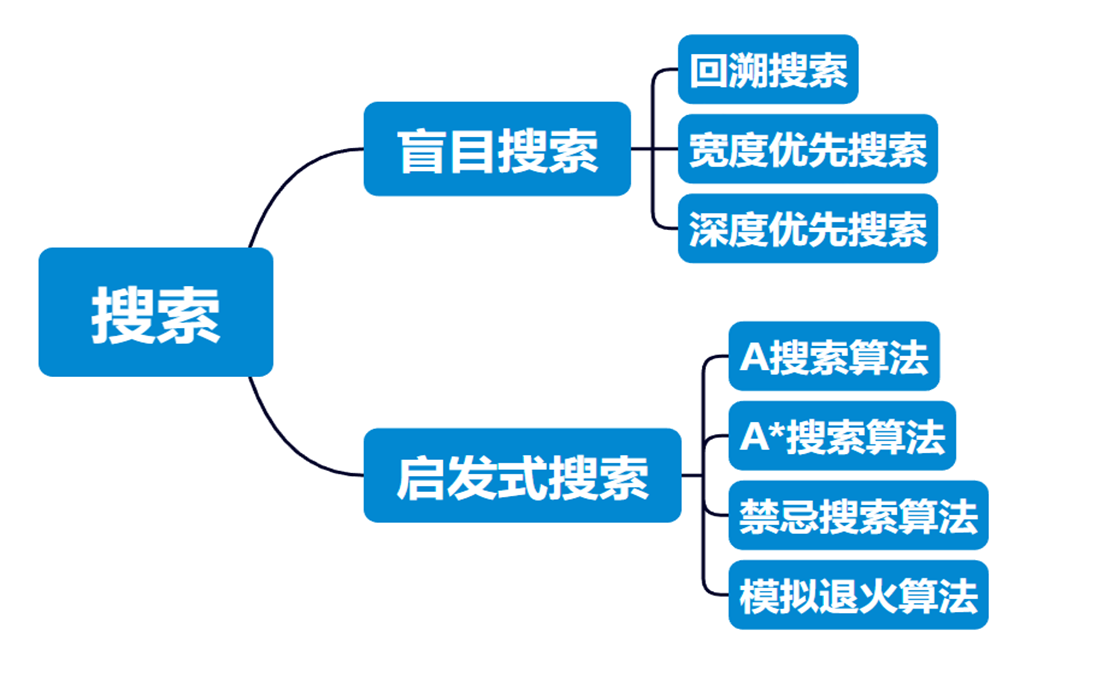
根据搜索过程是否使用启发式信息分为盲目搜索与启发式搜索。
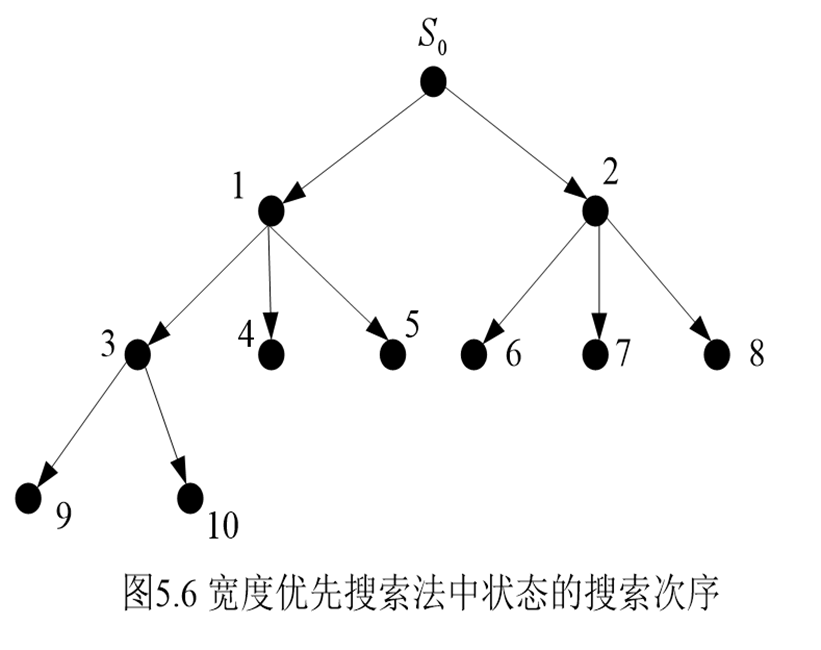
宽度优先搜索(BFS):从节点S0开始,对它的后续节点按从左至右搜索,然后再对下一级的后续节点按从左至右搜索,依次下去,直到搜索到目的状态。
- 当问题有解时,一定能找到解,而且能得到最优解
- 方法与问题无关,具有通用性
- 搜索节点数增加很快,所需空间和花费时间多
使用宽度优先搜索解决八数码问题
深度优先搜索(DFS):从节点S0开始,沿一个方向一直扩展下去,直到达到一定的深度。如果未找到目的状态或无法再扩展时,便回溯到另一条路径继续上述方法进行搜索。
- 一般不能保证找到最优解
- 当深度限制不合理时,可能找不到解
- 方法与问题无关,具有通用性
最坏情况下,搜索空间等同于穷举
使用深度优先搜索解决八数码问题(深度界限为4)
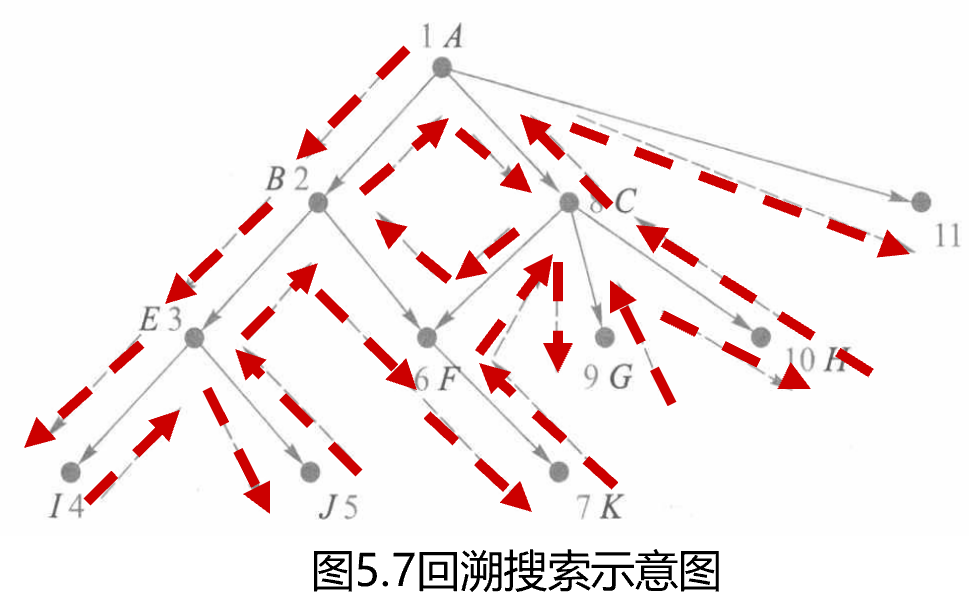
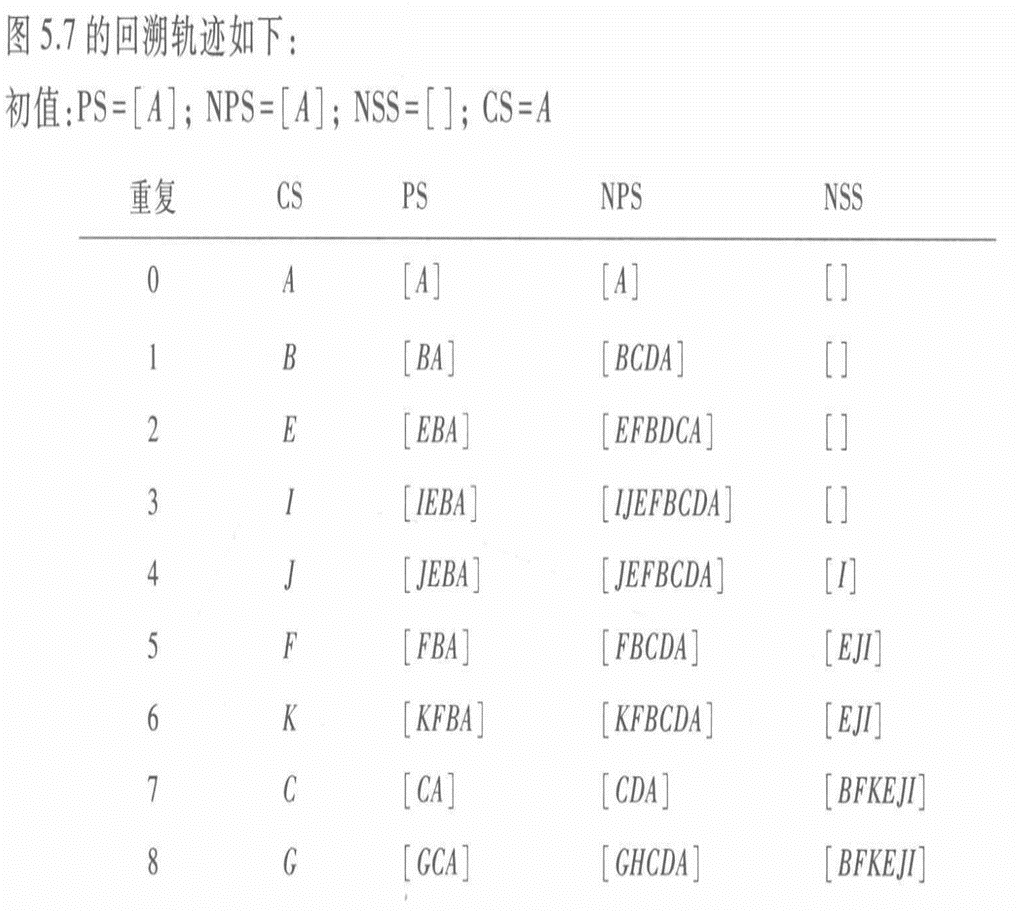
带回溯策略的搜索:当搜索到某一节点的时候,如果我们发现当前节点(及其子节点)并不是目标节点时,回退到原来的节点继续搜索,直到找到目标节点。深度优先搜索具有回溯的思想。
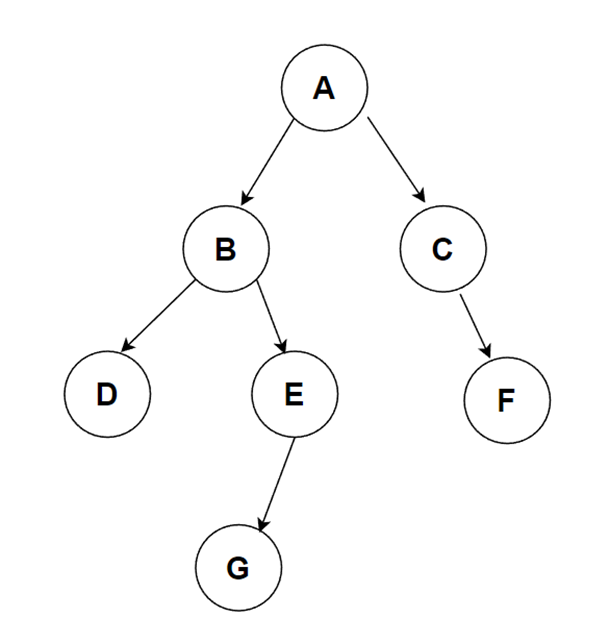
OPEN表:用来存放将要扩展的节点
CLOSED表:用来存放已经扩展的节点
| OPEN表 | CLOSED表 |
|---|---|
| {A} | { } |
| {B,C} | {A} |
| {D,E,C} | {A,B} |
| {E,G,C} | {A,B,D} |
| {G,C} | {A,B,D,E} |
| {C,F} | {A,B,D,E,G} |
| {F} | {A,B,D,E,G,C} |
| { } | {A,B,D,E,G,C,F} |
图搜索算法(宽度优先、深度优先、最好优先搜索等)都有回溯的思想。
- 概念:与具体问题求解过程有关的,并可指导搜索过程朝着最有希望的方向前进的控制信息。
- 作用:启发信息的启发能力越强,扩展的无用节点就越少。
- 陈述性启发信息:用于更准确、更精炼地描述状态
- 过程性启发信息:用于构造操作算子
- 控制性启发信息:表示控制策略的知识
- 用于扩展节点的选择,决定应先扩展哪一个节点,避免盲目扩展。
- 用于生成节点的选择,决定要生成哪些后继节点,以免盲目生成过多无用的节点。
- 用于删除节点的选择,决定删除哪些无用节点,以免造成进一步的时空浪费。
启发式搜索策略:利用与问题有关的启发信息引导搜索。
启发式图搜索策略的特点:重排OPEN表,选择最有希望的节点加以扩展。
运用启发式策略的两种基本情况:一个问题由于存在问题陈述和数据获取的模糊性,可能会使它没有一个确定的解。虽然一个问题可能有确定解,但是其状态空间特别大,搜索中生成扩展的状态数会随着搜索的深度呈指数级增长。
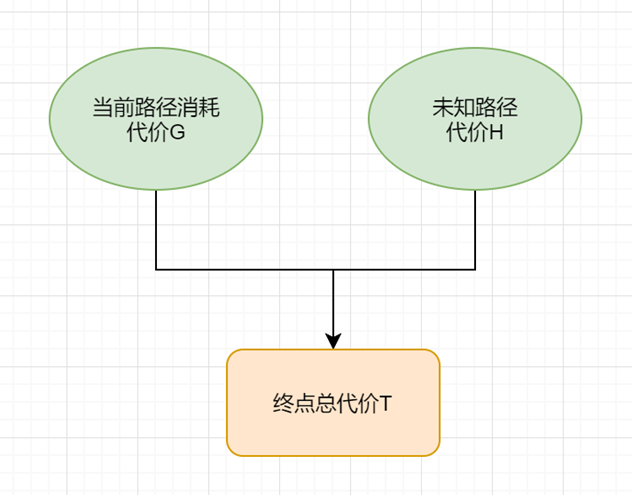
启发式策略的作用:通过引入估价函数值f(n) = g(n) + h(n),对状态空间中的每一步进行评估,获得最有可能在最终路线上的下一个点。因为估价函数的存在,每一步会优先向终点方向进行移动。
估价函数(evaluation function):评估节点“希望”程度或总代价的量度。
估价函数值f(n):从初始节点经过n节点到达目的结点的路径的最小代价估计值,其一般形式是:f(n) = g(n) + h(n)
g(n):起点到当前位置的实际路径长度,即从初始节点S0到节点n的实际代价;
h(n):从节点n到目标节点Sg的最优路径的估计代价,称为启发函数。
讨论启发函数h(n)取值对算法的影响
h(n)比重大:可以有效降低搜索工作量,但也会缩小探索范围,可能导致找不到最优解。当h(n)越复杂,即约束的条件越多,耗费的时间就越多;而减少约束条件,则可能得到的并不是最优路线。
h(n)比重小:一般导致工作量加大,极限情况下变为盲目搜索,搜索空间会比较大,但容易找到最优解。h(n)=0时,意味着此时是盲目搜索。
满足以下条件的算法为A*搜索算法:
- 使用估价函数f(n)=g(n)+h(n)对OPEN表中的节点按从小到大排序。
- 代价函数g(n)是对g(n)的估计,且g(n)>0。
- h(n)是h(n)的下界,即对所有的节点n均有:h(n)≤h(n)。
优点:如果某一问题有解,那么利用A搜索算法对该问题进行搜索则一定能搜索到解,并且一定能搜索到最优的解而结束。
缺点:A算法需要存储搜索过程中的节点信息,因此当搜索的状态空间较大时,它需要占用较大的存储空间。
| 算法名称 | 核心思想 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|
| 广度优先算法 | 不考虑每一步的移动成本,不断拓展边界,直到边界到达目标点 | 通常耗费大量时间 | 较大 |
| Dijkstra算法 | 以BFS为基础,只考虑每一点的总移动成本 | 通常耗费大量时间 | 一般 |
| 贪婪优先搜索 | 只考虑到达终点的估计距离,能较快寻找到目标 | 无法保证路线全局最优 | 一般 |
| A*搜索算法 | 以BSF为基础,综合考虑了总移动成本和到达终点的估计距离 | 具有更好的时间性能 l巧妙地叠加了“Dijkstra算法的成本最低”和“贪婪优先搜索的速度最优” | 需要存储搜索过程中的节点信息 当搜索的状态空间较大时,需占用较大存储空间 |