上一章:讨论了“知识与知识表示”,可以把知识用某种模式表示出来存储到计算机中,但为使计算机具有智能,还必须使它具有思维能力。
本章:1)推理是求解问题的一种重要方法。因此,推理方法成为人工智能的一个重要研究课题。2)目前已提出多种可在计算机上实现自动推理的方法。
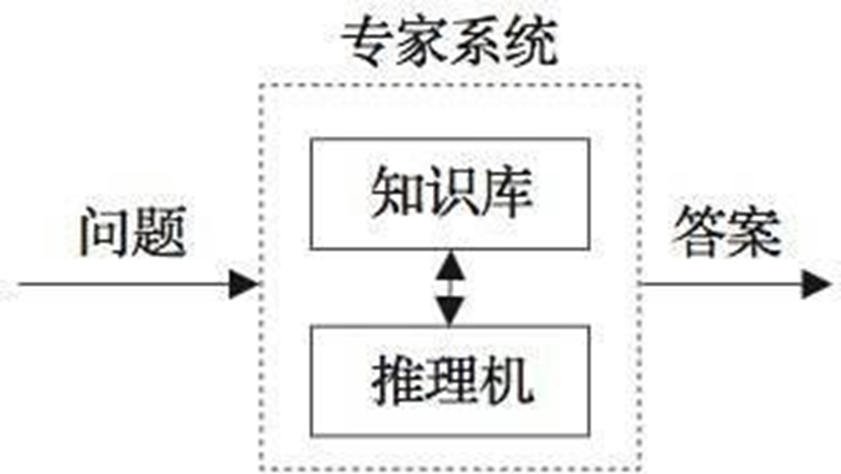
推理:从初始证据(已知事实)出发,按某种策略或规则,不断运用知识库中的已知知识,逐步推出结论的过程,或者归纳出新事实的思维过程。
两个基本要素:
- 事实/证据:推理的出发点、推理时应该使用的知识
- 知识:使推理得以向前推进,并逐步达到最终目标的依据
推理机:在AI系统中,推理过程通常由推理机来实现,它通常是一组程序,用来控制协调整个系统。
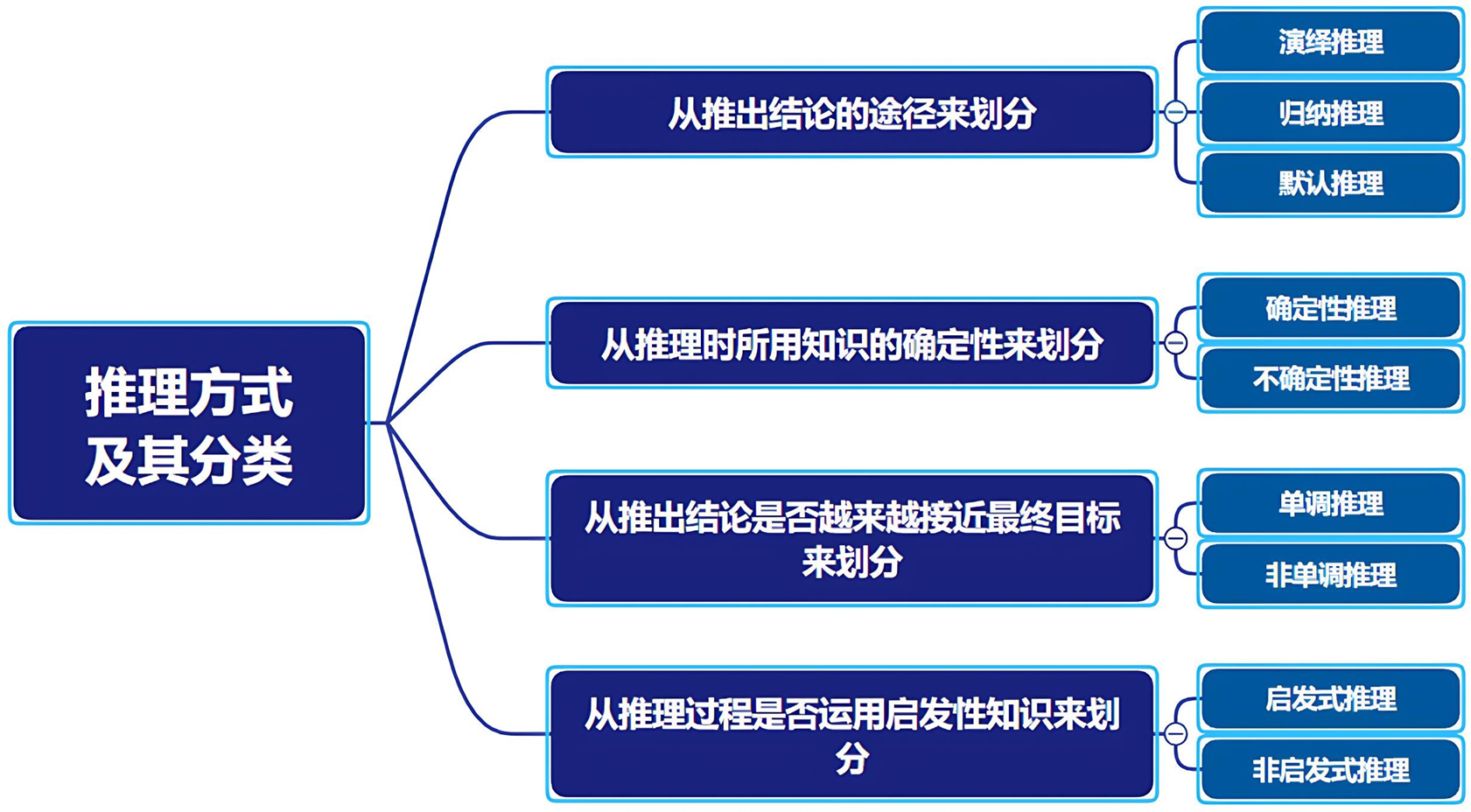
由一般性知识推出适合于某一具体情况的结论。
形式:三段论式
大前提:已知的一般性知识或假设。
小前提:关于所研究的具体情况或个别事实的判断。
结论:由大前提推出的适合于小前提所式情况的新判断。
从足够多的事例中归纳出一般性结论的推理过程。
完全归纳推理和不完全归纳推理:
完全归纳推理(必然性推理):考察了相应事物的全部对象,就得出了结论。
不完全归纳推理(非必然性推理):考察了相应事物的部分对象,就得出了结论。
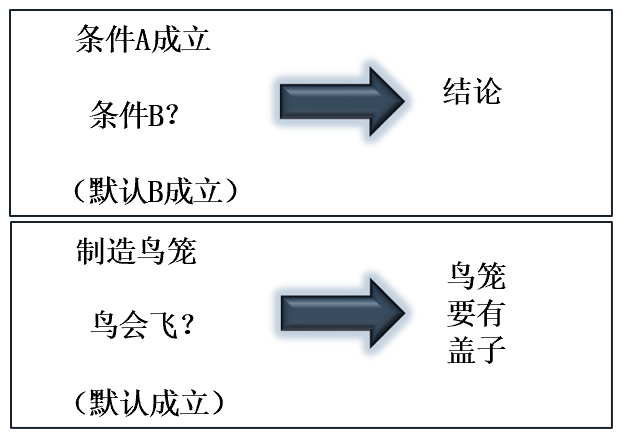
是在知识不完全的情况下假设某些条件已经具备所进行的推理。发现原先所做的默认不正确,则要撤销所做的默认以及由此默认推出的所有结论,重新按新情况进行推理。
推理时所用的知识与证据都是确定的,推出的结论也是确定的,即真值为真或者为假。
经典逻辑推理是确定性推理
推理时所用的知识与证据不都是确定的,推出的结论也是不确定的
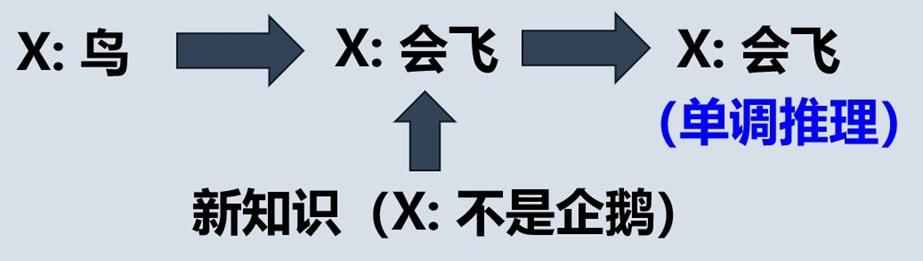
随着推理向前推进及新知识的加入,推论不断加强,推出的结论越来越接近最终目标。
由于新知识的加入,不仅没有加强已推出的结论,反而要否定它,使推理退回到前面的某一步,重新开始。
运用与推理有关的启发性知识
没有运用与推理有关的启发性知识
启发性知识:与问题有关且能加快推理过程、求得问题最优解的知识。
基本思想:以已知事实作为出发点的一种推理。
优点:简单,易实现。
缺点:目的性不强,效率低。
基本思想:以某个假设目标作为出发点的一种推理。
优点:不必使用与目标无关的知识,目的性强,还有利于向用户提供解释。
缺点:起始目标的选择有盲目性。
以下情况,常需采用混合推理:已知的事实不充分。(先正后逆)正向推理退出的结论可信度不高。(先正后逆)希望得到更多的结论。(先逆后正)
基本思想:双向同时进行,且在某一步骤上“碰头”。
特点:即由正向推理所得到的中间结论,恰好是逆向推理此时所要求的证据。
已知事实与知识进行匹配,可能发生的三种匹配情况:
- 恰好匹配成功(一对一)
- 不能匹配成功
- 多种匹配成功(一对多、多对一、多对多)。这种情况会产生冲突,因此需要一定的策略解决
- 按规则的针对性排序
- 按已知事实的新鲜性排序
- 按匹配度排序
- 按条件个数排序
定义:由已知的普遍性知识或前提出发,通过推导(即 “演绎”)得出具体陈述或特殊性结论的推理(即从一般到个别)。
主要包括:三段论、假言推理、选言推 理等。
缺点:不能产生新知识。
定义:从大量的事例中总结出一般性结论的推理过程,是一种从个别到一般的推理,从特殊的前提推出普遍结论的推理。
更一步的细分类见下页。
定义:在知识不完全的情况下作出的推理。
特点:允许默认某
些条件成立,摆脱了需知道全部有关事实才能进行推理的要求,使得在知识不完全的情况下也能进行推理。
基本思想:从一组已知为真的事实出发,直接运用经典逻辑(命题逻辑、谓词逻辑)中的推理规则,推出结论的过程。
优点:推理过程灵活便于嵌入领域启发式知识。
缺点:易产生组合爆炸,不利于复杂问题的推理
| 大类 | 细项 | 演绎推理 | 归纳推理 |
|---|---|---|---|
| 区别 | 推理方向不同 | 一般到个别 | 个别到一般 |
| 前提数量不同 | 相对有限 | 不确定 | |
| 结论断定范围不同 | 没有超出前提所提供的知识范围 | 超出 | |
| 前提与结论的联系 不同 | 必然联系 | 不一定有联 系 | |
| 联系 | l演绎必须以归纳为基础(演绎推理如果要以一般性知识为前提,那么这些知识通常由归纳推理得出) l归纳必须以演绎为指导 l归纳和演绎推理互相渗透和转化。 |
基本思想:基于反证法,证明所证公式会假时会产生矛盾,从而说明所证公式为真。
对比:1)自然演绎推理是从已知为真的事实出发,运用经典逻辑的推理规则导出结论;2)而归结演绎推理的思路恰好与之相反。
定理证明过程:
正向即证明P→Q即“(¬P∨Q)的永真性”。根据反证法,只要证明其反面“(P∧¬Q)
的不可满足性”即可。
海伯伦(Herbrand)定理:为自动定理证明奠定了理论基础;
鲁滨逊(Robinson)归结原理:使机器定理证明成为现实。
原来:判断一个子句的不可满足性,需要对个体域上的一切解释逐
个进行判定,只有当子句对任何非空个体域上的任何一个解释都是不可满足的,该子句才是不可满足的。
优化后:海伯伦构造了一个特殊的域(海伯伦域),并证明只要对这个特殊域上的一切解释进行判定,就可知子句集是否不可满足。
缺点:海伯伦理论的计算量会呈指数增长,用它来计算不现实。
基本概念
谓词公式的永真式(重言式,Taotology)
谓词公式的可满足(Satisfiable)
谓词公式的永假式(Contradiction/Unsatisfiable)
谓词公式的范式:公式的标准形式,有前束范式、斯科伦范式。
谓词公式化为子句集
前束范式(Prenex Normal Form)
斯科伦范式(Skolem Standard Form)
原理内容:鲁滨逊在海伯伦理论的基础上,对子聚集中的子句做逐次归结来证明子句集
的不可满足性(如果子句集中各子句相互矛盾),提出归结原理,成为机器证明基础。
基本思想:
由谓词逻辑转化的子句集中的子句之间是合取关系,只要有一个子句不满足,则整个子句集不满足;
如果一个子句集中包含有空子句,则该子句集一定不可满足。
实现思路:通过归结方法不断扩充判定的子句集,并设法使其包含进指示矛盾(即永假)的子句,从而说明子句集不满足。
基本方法:1)检查子句集S中是否包含空子句,若包含,则S不可满足;2)若不包含,就在子句集中选择合适的子句进行归结,一旦通过归结得到空子句,就说明S是不可满足的。
归结反演:应用归结原理证明定理的过程。
一般步骤:
1将“已知前提”表示为谓词公式F。
2将“待证明的结论”表示为谓词公式Q ,并否定得到¬ Q 。
3把谓词公式集{𝐹, ¬𝑄}化为子句集S。
4应用归结原理对S中的子句进行归结,把每次归结得到的归结式都并入到S中。
反复进行,若出现了空子句,则停止归结,此时就证明了Q为真。
招聘工作人员,A,B,C三人应试,经面试后公司表示如下想法:
1三人中至少录取一人。
2如果录取A而不录取B,则一定录取C。
3如果录取B,则一定录取C。
求证:公司一定录取C。
一般步骤:
设用谓词P(x)表示录取x,则把公司的想法用谓词公式表示为:
(1)P(A)∨P(B)∨P(C) (2)P(A)∧¬P(B)→P(C) (3) P(B)→P(C)
把要求证的结论用谓词公式表示出来并否定,得(4)¬P(C)
把上述公式化成子句集:
(1)P(A)∨P(B)∨P(C) (2) ¬P(A)∨P(B)∨P(C) (3)¬P(B)∨P(C) (4)¬P(C)
应用归结原理进行归结:
(5)P(B)∨P(C) (1)与(2)归结 (6)P(C) (3)与(5)归结 (7)NIL (4)与(6)归结
所以公司一定录取C