——作者:木人舟
- anaconda3,集成了常用的用于科学计算的包,以及python解释器(本例使用的解释器版本为3.11.5)
- 编辑器或者IDE:Vscode或者pycharm
本文将SGA遗传算法按照ppt的编写分为八个模块(python文件)进行阐述
分别是:
- geneEncoding.py
- ga.py(主功能模块,运行此模块即可运行遗传算法)
- best.py
- calfitValue.py
- calobjValue.py
- crossover.py
- mutation.py
- selection.py
具体的流程图解释如下:
-
种群初始化:对参数进行编码,适应度函数的设计,以及初始群体的设定
-
适应度计算:为每次群体中的个体赋予适应度,方便后面遗传操作的进行
-
选择操作:对群体进行选择,选择出适应度值较大的一部分优势群体;
-
交叉操作:对优势种群进行 “交配”,更容易产生优秀的个体;
-
变异操作:对染色体中的基因用一定的变异方法进行变异
下面以计算函数最大值为例,阐述SGA的具体步骤 $$ f(x)=10sin5x + 7cos4x $$
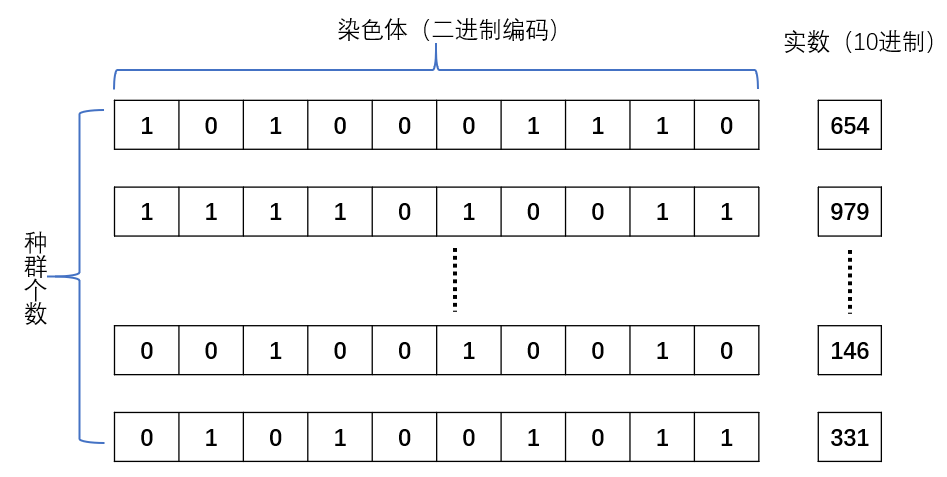
在本例中,染色体的编码方式采用二进制编码,即用若干二进制数表示一个个体,将原问题的解空间映射到位串空间B={0,1}上
相应模块geneEncoding.py如下
import random
"""
@brief 生成一个二元组的种群,其中种群内的个体以二进制的形式来表示
@param pop_size 整个种群的个体数量
chrom_length 染色体的长度,其实就是二元组内元素的二进制数的个数,
比如当chrom_length=4,种群内的一个个体可以表示为[1,1,0,1]
@retval 返回一个种群,由于初始化时第一个元素是空列表[],因此返回的是pop[1:]
"""
def geneEncoding(pop_size, chrom_length):
pop = [[]]
for i in range(pop_size):
temp = []
for j in range(chrom_length):
temp.append(random.randint(0, 1))
pop.append(temp)
return pop[1:]
# 测试部分
if __name__ == "__main__":
pop_size = 5 # 种群数量
chrom_length = 2 # 染色体长度
pop = geneEncoding(pop_size, chrom_length)
print(pop, "\n")
print(len(pop), "\n")可以注意到,经过编码生成后的种群,可以看作是一个二维矩阵,其中矩阵的size=(种群大小,染色体编码长度)
适应度函数得出的值越大表明个体越优秀,所以一般情况下,在求解函数最大值的时候,适应度函数就是求解函数本身,求解最小值的时候适应度函数就是函数的倒数。在本例中求取最大值,所以适应度函数就是函数本身。
相应模块calobjValue.py内容如下
import math
"""
@brief 解码,将传进来的二进制序列转换成十进制
@param pop_size 种群的个体数量
chrom_length 染色体的长度
@retval 十进制序列
"""
def decodechrom(pop, chrom_length):
temp = []
for i in range(len(pop)):
t = 0
for j in range(chrom_length):
t += pop[i][j] * (math.pow(2, j))
temp.append(t)
return temp
"""
@brief 根据适应度函数,计算种群中个体的适应度
@param pop 种群,一个二元组
chrom_length 染色体的长度
max_value 染色体长度允许的最大值
@retval 个体适应度的列表
"""
def calobjValue(pop, chrom_length, max_value):
temp1 = []
obj_value = []
# 将pop解码
temp1 = decodechrom(pop, chrom_length)
for i in range(len(temp1)):
x = temp1[i] * max_value / (math.pow(2, chrom_length) - 1)
# 适应度函数
obj_value.append(10 * math.sin(5 * x) + 7 * math.cos(4 * x))
return obj_value
# 测试部分
if __name__ == "__main__":
pop_size = 5 # 种群数量
pop = [[0, 0, 1], [0, 1, 0], [1, 0, 0]]
test = calobjValue(pop, 3, 10)
print(test)在上一步根据适应度函数计算出个体相应的适应度之后,得出来的结果中,有些个体对应的适应度会是负值
说明这些个体,是不适合**“生存”**的,我们需要将这部分适应度为负值的个体进行淘汰和去除
具体方法如calfitValue.py所示:
"""
@brief 对种群中不适合的个体进行淘汰,其实就是去除负值
@param obj_value 个体适应度的列表
@retval 个体适应度淘汰后的列表
"""
def calfitValue(obj_value):
fit_value = []
c_min = 0
for i in range(len(obj_value)):
if obj_value[i] + c_min > 0:
temp = c_min + obj_value[i]
else:
temp = 0.0
fit_value.append(temp)
return fit_value
if __name__ == "__main__":
pass在上一步去除掉本次迭代中的不适应个体后,我们需要从当前种群中保存本次迭代中的最优个体以及对应的基因,这里采取的方法是直接从适应度列表中找一个适应度最大的个体
具体实现如模块best.py
"""
@brief 找出最优解和最优解的基因编码
@param pop 种群,一个二元组
fit_value 适应度列表
@retval 最优解及其基因
"""
def best(pop, fit_value):
best_individual = []
best_fit = fit_value[0]
for i in range(1, len(pop)):
if fit_value[i] > best_fit:
best_fit = fit_value[i]
best_individual = pop[i]
return [best_individual, best_fit]
if __name__ == "__main__":
pass个体选择的方法有很多种(可以自己参照前面的ppt),在我这个例子中,我采用是轮盘赌选择算法
注: 在本例中选择后的种群个体数目和原种群个数相同。
具体实现如selection.py模块
import random
# 计算种群中所有个体的适应度总和
def sum(fit_value):
total = 0
for i in range(len(fit_value)):
total += fit_value[i]
return total
# 计算累积概率
def cumsum(fit_value):
for i in range(len(fit_value) - 2, -1, -1):
t = 0
j = 0
while j <= i:
t += fit_value[j]
j += 1
fit_value[i] = t
fit_value[len(fit_value) - 1] = 1
"""
@brief 对种群进行选择复制
@param pop 种群,一个二元组
fit_value 适应度列表
@retval 新的种群
"""
def selection(pop, fit_value):
# 存放每个个体被选择的概率的列表,采用的分配方法是适应度比例方法
newfit_value = []
# 适应度总和
total_fit = sum(fit_value)
for i in range(len(fit_value)):
newfit_value.append(fit_value[i] / total_fit)
# 计算累计概率
cumsum(newfit_value)
ms = []
pop_len = len(pop)
for i in range(pop_len):
ms.append(random.random())
ms.sort()
fitin = 0
newin = 0
newpop = pop
# 转轮盘选择法
while newin < pop_len:
if ms[newin] < newfit_value[fitin]:
newpop[newin] = pop[fitin]
newin = newin + 1
else:
fitin = fitin + 1
pop = newpop
# 测试部分
if __name__ == "__main__":
pop = [[0, 0, 1], [0, 0, 0], [0, 1, 0]]
fit = [4, 4, 2]
print(pop)
selection(pop, fit)
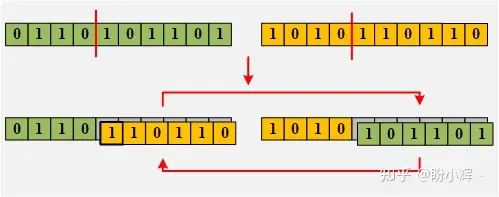
print(pop)交叉方法我在这个例子中选择的是单点交叉(Single-point-Crossover),单点交叉就是随机选择双亲染色体上的位置。此位置称为交叉点 (crossover point) 或切割点 (cut point)。该点右边的基因在双亲染色体之间交换,得到了两个后代,每个后代都携带着双亲的一些遗传信息。可以配合图像理解
程序实现见crossover.py模块
import random
"""
@brief 采用单点交叉
@param pop 种群,一个二元组
pc 交叉概率
@retval none
"""
def crossover(pop, pc):
for i in range(len(pop) - 1):
if random.random() < pc:
cpoint = random.randint(0, len(pop[0]))
temp1 = []
temp2 = []
temp1.extend(pop[i][0:cpoint])
temp1.extend(pop[i + 1][cpoint : len(pop[i])])
temp2.extend(pop[i + 1][0:cpoint])
temp2.extend(pop[i][cpoint : len(pop[i])])
pop[i] = temp1
pop[i + 1] = temp2
if __name__ == "__main__":
pass变异方式我在本例中采取的是位点变异,具体思想就是在染色体的一串基因中,随机找一个位置上的基因进行按位取反(因为采用的编码格式是二进制编码)
程序实现见mutation.py
import random
"""
@brief 采用的变异方法是随机单点变异,意思就是随机在染色体上找一个基因进行按位取反
@param pop 种群,一个二元组
pm 变异概率
@retval none
"""
def mutation(pop, pm):
for i in range(len(pop)):
if random.random() < pm:
mpoint = random.randint(0, len(pop[0]) - 1)
# 进行按位取反
if pop[i][mpoint] == 1:
pop[i][mpoint] = 0
else:
pop[i][mpoint] = 1
if __name__ == "__main__":
pass介绍完以上七个功能模块就能对主程序进行编写了
具体实现见ga.py
import matplotlib.pyplot
import math
from calobjValue import calobjValue
from calfitValue import calfitValue
from selection import selection
from crossover import crossover
from mutation import mutation
from best import best
from geneEncoding import geneEncoding
print("适应度函数为:y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x)")
# 计算2进制序列代表的数值
def b2d(b, max_value, chrom_length):
t = 0
for j in range(len(b)):
t += b[j] * (math.pow(2, j))
t = t * max_value / (math.pow(2, chrom_length) - 1)
return t
pop_size = 500 # 种群数量
max_value = 10 # 基因中允许出现的最大值
chrom_length = 10 # 染色体长度
pc = 0.1 # 交叉概念
pm = 0.01 # 变异概率
results = [[]] # 存储每一代的最优解,N个二元组
fit_value = [] # 个体适应度
fit_mean = [] # 平均适应度
# pop = [[0, 1, 0, 1, 0, 1, 0, 1, 0, 1] for i in range(pop_size)]
pop = geneEncoding(pop_size, chrom_length)
for i in range(pop_size):
obj_value = calobjValue(pop, chrom_length, max_value) # 个体评价
fit_value = calfitValue(obj_value) # 淘汰
best_individual, best_fit = best(pop, fit_value) # 第一个存储最优的解, 第二个存储最优基因
results.append([best_fit, b2d(best_individual, max_value, chrom_length)])
selection(pop, fit_value) # 新种群复制
crossover(pop, pc) # 交配
mutation(pop, pm) # 变异
# 初始化的时候,第一个元素是空列表,所以要进行排除
results = results[1:]
results.sort()
print(results)
print("y = %f, x = %f\n" % (results[-1][0], results[-1][1]))
X = []
Y = []
for i in range(pop_size):
X.append(i)
t = results[i][0]
Y.append(t)
# 将得到的results二元组以可视化的形式展现出来
matplotlib.pyplot.plot(X, Y)
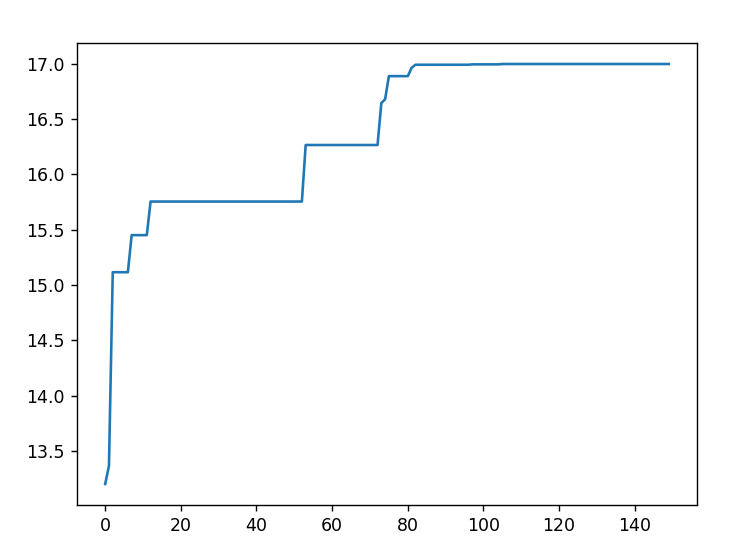
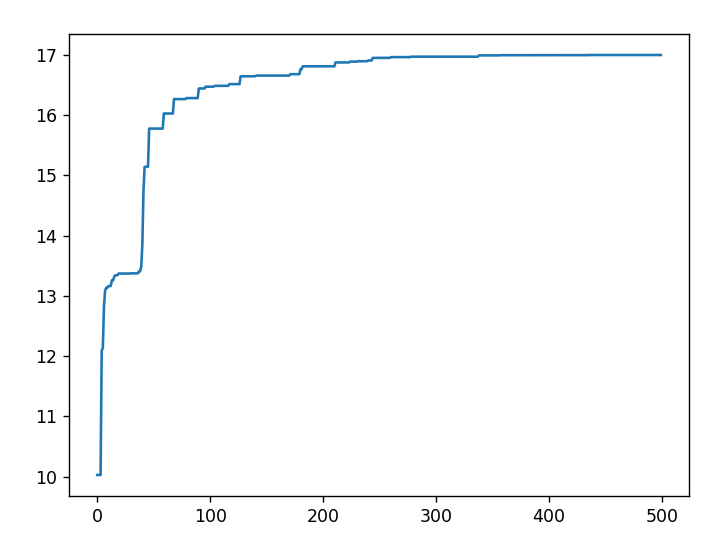
matplotlib.pyplot.show()横坐标为迭代次数,纵坐标为求解结果
迭代次数n=50
迭代次数n=150
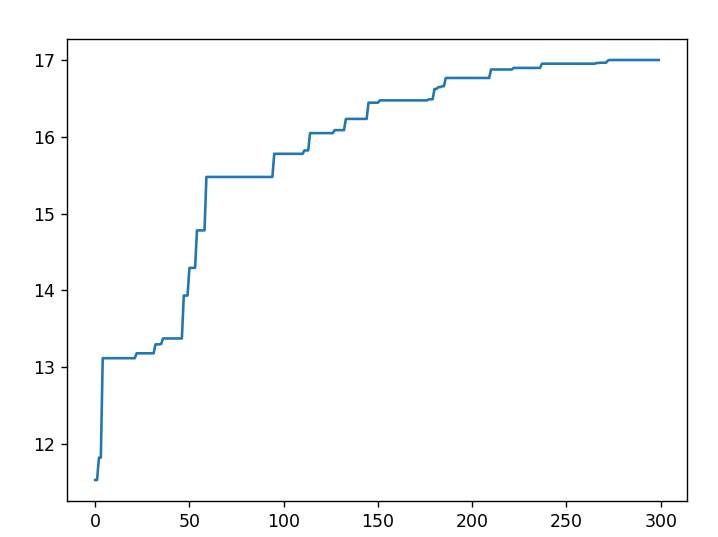
迭代次数n=300
迭代次数n=500
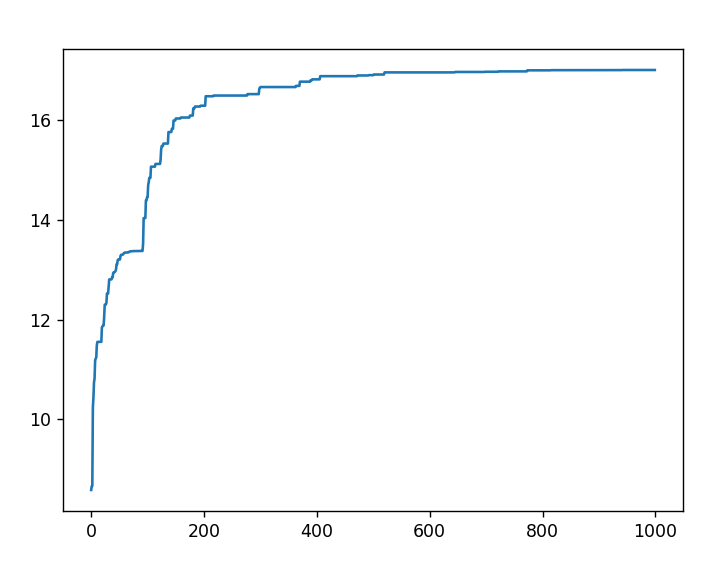
迭代次数n=1000
经过多次的结果运行中,我们可以下结论:
函数 $$ f(x)=10sin5x + 7cos4x $$ 的最大值为17,同学们也可以自己通过数学运算,验证这一结果
当迭代次数过少的时候,SGA很容易陷入局部最优解中,但是当迭代次数很多的时候,比如上图测试迭代次数n=1000的结果中,运行时间相当的长(在我自己电脑中有1分钟左右)。所以SGA虽然说操作简单,但是也有非常明显的短板