本文算是我学习这个算法的学习记录,因此我会更加侧重于程序实现的讲解,因为原理相关的内容我已经非常熟悉了,并且Dijkstra算法需要有一定图论相关的知识,不过没必要完全系统地学会,只需要知道无向图,有向图,邻接矩阵相关的概念就行了。
下面我将会以在图中寻找一个节点(称为“源节点”)到所有其它节点的最短路径的例子进行讲解,在文章的末尾将给出程序完整的Python与C++实现
下面的相关知识,是你在编程前必须要知道的
-
Dijkstra 算法从指定的节点(源节点)出发,寻找它与图中所有其它节点之间的最短路径。
-
Dijkstra 算法会记录当前已知的最短路径,并在寻找到更短的路径时更新。
-
一旦找到源节点与其他节点之间的最短路径,那个节点会被标记为“已访问”并添加到路径中。
-
重复寻找过程,直到图中所有节点都已经添加到路径中。这样,就可以得到从源节点出发访问所有其他节点的最短路径方案。
-
Dijkstra 只能用在权重为正的图中,因为计算过程中需要将边的权重相加来寻找最短路径。
Dijkstra算法可以看成是贪心策略与广度优先算法的结合,在每一次节点扩散的时候,都需要进行权重(可以理解为距离)大小的比较,因此存在负权重,则可能在之后的计算中得到总权重更小的路径,从而影响之前的结果,用一个比较实际的例子就是绕的路更多,反而路线更短了,这显然是不符合实际的
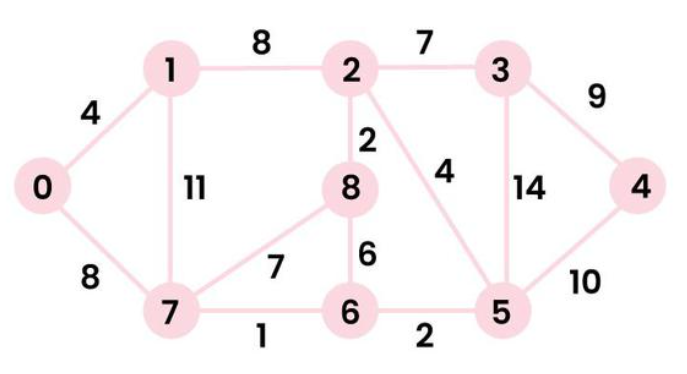
假设有下面这个图,我们设置源节点 src=0,为了求解src到其他节点(1~8)的最短距离,按照下面的步骤
- 这里我们需要维护两个数组isset和dist,其中isset数组用来表示对应节点是否已经拓展,初始化为
false。dist数组初始化为{0, INF, INF, INF, INF, INF, INF, INF},这个数组的下标用来表示节点,下标对应的内容表示src节点到其他节点的最短距离,这里选取的src=0,由于节点到自身的距离始终为0,所以这里dist[0]=0,其他初始化为INF(无穷大)
#参数初始化
dist = [float('inf')] * len(graph)
isset = [False] * len(graph)
dist[src] = 0- 现在我们需要从dist数组中找到距离值最小且isset数组值为false的节点,由于是第一次扩展节点,所以距离值最小的一定是src节点。扩展后将src节点下标对应的isset数组的内容改为
true,0 的相邻顶点是 1 和 7,更改距离值.
#寻找dist最小值
def MinDistance(dist, isset):
min = float('inf')
min_index = 0
for v in range(len(dist)):
if isset[v] == False and dist[v] <= min:
min = dist[v]
min_index = v
return min_index
#将拓展的节点标记为True
min_index = MinDistance(dist, isset)
isset[min_index] = True| isset | true | false | false | false | false | false | false | false | false |
|---|---|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dist | 0 | 4 | INF | INF | INF | INF | INF | 8 | INF |
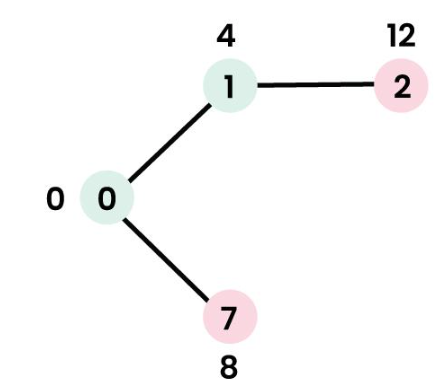
- 接着从dist数组中找出最小值且isset数组值为false的节点进行扩展,在第二步得到的结果中,dist最小值对应的是节点
1,因此对节点1的相邻节点进行扩展,然后将节点2的值更改为12,为什么是12而不是8?,参照上面完整的图,节点0到节点1的距离是4,节点1到节点2的的距离是8,所以这里的12指的是经过0-1-2的累加距离4+8=12,后面每次扩展的时候,都要进行距离的累加
# 整个算法最核心的部分就是这个if的判断语句
if not isset[v] and graph[min_index][v] > 0 and dist[min_index] != float('inf') and dist[min_index] + graph[min_index][v] < dist[v]:
dist[v] = dist[min_index] + graph[min_index][v]经过上述的变化后,数组的值变更为以下的结果
| isset | true | true | false | false | false | false | false | false | false |
|---|---|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dist | 0 | 4 | 12 | INF | INF | INF | INF | 8 | INF |
- 重复以上的步骤,这里需要注意如果新扩展到的dist数组的值比旧的dist数组的值要大,那么就不更新dist数组
- 最终可以得到一个src节点到其他节点的最小生成树
接下来将代码整合成一个完整版
import numpy as np
# 这个函数用来求解dist中距离值最小且isset为false的节点
def MinDistance(dist, isset):
min = float('inf')
min_index = 0
for v in range(len(dist)):
if isset[v] == False and dist[v] <= min:
min = dist[v]
min_index = v
return min_index
# 算法的实现部分
def Dijkstra(graph:list|np.ndarray, src:int):
#初始化dist和isset的值
dist = [float('inf')] * len(graph)
isset = [False] * len(graph)
dist[src] = 0
for i in range(len(graph) - 1):
min_index = MinDistance(dist, isset)
isset[min_index] = True
for v in range(len(graph)):
# 算法核心部分,最重要的是判断dist[min_index] + graph[min_index][v] < dist[v]
if not isset[v] and graph[min_index][v] > 0 and dist[min_index] != float('inf') and dist[min_index] + graph[min_index][v] < dist[v]:
dist[v] = dist[min_index] + graph[min_index][v]
for i in range(len(dist)):
print("节点",i, ":",dist[i])
if __name__=='__main__':
# 用来测试的图,邻阶矩阵表示,如果不熟悉numpy,替换成python自带的list类型也行
graph = np.array([
[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]])
print("打印dist数组")
Dijkstra(graph, 1)
# 运行结果
"""
打印dist数组
节点 0 : 4
节点 1 : 0
节点 2 : 8
节点 3 : 15
节点 4 : 22
节点 5 : 12
节点 6 : 12
节点 7 : 11
节点 8 : 10
"""#include <iostream>
#include <algorithm>
#include <vector>
#include <list>
#include <chrono>
using std::cerr;
using std::cin;
using std::cout;
using std::endl;
using std::string;
int MinDistance(std::vector<double> &dist, std::vector<bool> &isset)
{
// 初始化最小值
double min = std::numeric_limits<double>::max();
int min_index;
for (int v = 0; v < dist.size(); v++)
if (isset[v] == false && dist[v] <= min)
min = dist[v], min_index = v;
return min_index;
}
void Dijkstra(std::vector<std::vector<double>> &graph, int src)
{
std::vector<double> dist(graph.size(), std::numeric_limits<double>::max());
std::vector<bool> isset(graph.size(), false);
// src与自身的距离始终为0,不需要进行计算
dist[src] = 0;
for (size_t i = 0; i < graph.size() - 1; i++)
{
int min_index = MinDistance(dist, isset);
isset[min_index] = true;
for (size_t v = 0; v < 9; v++)
{
if (!isset[v] && graph[min_index][v] && dist[min_index] != std::numeric_limits<double>::max() && dist[min_index] + graph[min_index][v] < dist[v])
{
dist[v] = dist[min_index] + graph[min_index][v];
}
}
}
// 打印距离数组
for (int i = 0; i < dist.size(); i++)
{
cout << i << ":" << dist[i] << endl;
}
}
void GraphTest(void)
{
//没用过vector的话,用普通的二维数组替换也行
std::vector<std::vector<double>> graph = {
{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 2},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 0, 10, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 6},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0}};
;
// 将给定的二维数组值赋给嵌套vector
Dijkstra(graph, 1);
}
int main(void)
{
GraphTest();
}