I want to evaluate every Mathematical Chess relative piece value and the best dealt target point

[ghost]

Hi .@ianfab. Hello all. Let me introduce you some new things.
This is Vietnamese Mathematical Chess—
http://cotoan.vnvista.com/rules-en.html
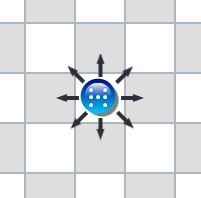
The board contains 11 ranks and 9 files. Each side has ten pieces, numbered from 0 to 9. The board initial layout is as displayed in the picture below—

Movements: Each piece (with the exception of 0 piece) can move in any direction (vertically, horizontally, or diagonally − forward or backward), the max number of squares a piece can move depends on the number of the piece.
For example, the piece with number 2 can move 1 or 2 empty squares, while the piece with number 9 can move from 1 to 9 empty squares—

Capture: To capture the opponent's piece, a player must have two pieces one next to another. Then use the numbers of the two pieces to make calculations. Allowed calculations are + (addition), - (subtraction), × (multiplication), ÷ (division), and modulus (division reminder).

Any results of the calculations can be used to apply to the capture. If a result contains two numbers, then remove the tens number (for example 8×7=56=>use 6). Use a suitable result to make the capture by taking the piece behind to capture the opponent's piece.

For example, one player have an 8 piece and 5 piece next to each other vertically. Calculation results from these 2 pieces are:
8+5=13 (take 3)
8-5=3
8×5=40 (take 0 - which is useless anyway)
8÷5=1 with 3 as remainder (take both 1 and 3)
The player can then use the 8 piece (the piece behind) to capture an opponent piece which is 1 or 3 squares away from the 5 piece (the piece in front), in the same the direction that 8->5 is.

72 and 49 are the two strongest combinations.

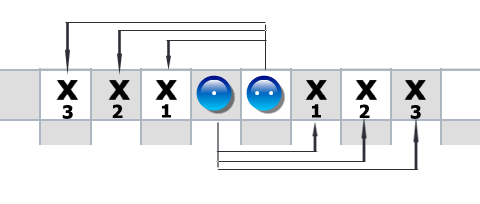
The image below shows how the 1 piece and 2 piece standing next to each other can capture the opponent's pieces. If an opponent's piece is on one of those X squares, the player can capture it. The calculations that the capture is based on are: 1+2=3, 1×2=2, 1÷2=0 with 1 as remainder—

The 0 piece (the one with zero number) is like the King in Chess. When it is captured, the player loses the game.

Besides capturing the 0 piece, players can agree at a certain point to end a match (if the 0 piece is not captured before that point is reached). The point that one player gains is calculated by summing the numbers of the opponent's pieces that have been captured.

For example, if the players agree to set the match's target "ending" point to 10. Then when a player captures the 5 and 6 piece, he wins the game (5+6=11 which is greater than 10). Or if a player captures the 0 piece then he also wins.

We all know that the aim of Chess is to checkmate the opponent's King, the aim of Go is to surround a larger total area of the board with one's stones than the opponent (count by scores). In Mathematical Chess, I think we must balance Chess and Go, and the game−complexity is really high.

I want to evaluate every Mathematical Chess relative piece value.

Currently, there are two Chess engine models. In the first, the traditional one going back fifty years, the engine is programmed with the previously known Chess piece values for use in positional evaluation. In the second, the AlphaZero model based on neural networks, the engine learns by playing against itself with perhaps a head start gained by putting in a large number of master games.
This suggests two possible approaches I could try.
The first obvious one is to program the neural net to play Vietnamese Mathematical Chess, and derive piece values from that once it reaches a certain level (I can't do that now).
The second one relies on having a very large database of Vietnamese Mathematical Chess games and using logistic regression. There is an interesting blog post by Rasmus Bååth in which he describes his efforts to derive from scratch the values of the chess pieces in the traditional game. How successful Rasmus Bååth's approach was is open to some doubt. He got that a queen was worth 4x a pawn, however that may be a reflection of his data rather than his methods. The relative value he obtained for the other pieces does correspond to traditional values. Unfortunately, there is no any research effort on this Chess-variant. The rule's point that I love most in Mathematical Chess is setting target point by dealt. That's like the first leg match played.

So if you have a bias towards the target point A, your opponent chooses B. In this situation, what dealt rule that could help?

Hope to see nice solutions (even elegant solutions).
Any comments and suggestions are welcome and appreciated.

[ianfab]

Hi. Usually in most chess variants capturing occurs by displacement, which is why the design of Fairy-Stockfish is mostly centered around that. However, for atomic chess there already is some logic that handles capturing pieces on a different square than the destination square, so you could have a look at that if you would like to experiment with implementing this variant.

[ghost]

Roger that, sir.