字典树是一种专门处理字符串设计的一种数据结构。我们先来说一下他的优点。在这里呢我们跟之前的讲的二分搜索或者其他树结构进行比较。
我们知道,我们采用树结构进行查询操作时,时间复杂度为O(log(N))。那么假设我们有100万个条目(2^20)。那么采用树结构的时间复杂度大约为20。那么小伙伴可能好奇,这个结构不已经很优化了吗,其实这种数据结构存储一般性数据或者对象来说已经很优秀了,但是字典树可以说是专门为处理字符串优化过的。因为我们在字典树中查询一个元素,时间复杂度就不取决于树本身的结构,而是取决于要查询字符串的长度。时间复杂度为 O(w) 。w是指字符串的长度。而且一般的单词长度都不会超过10,所以处理起来时间复杂度就会很低。
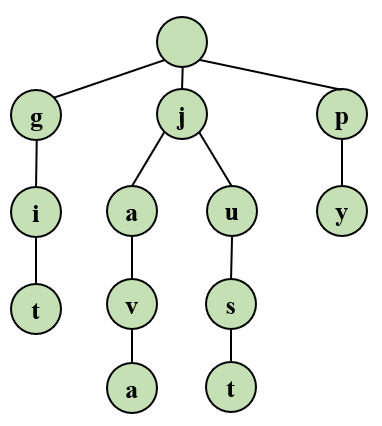
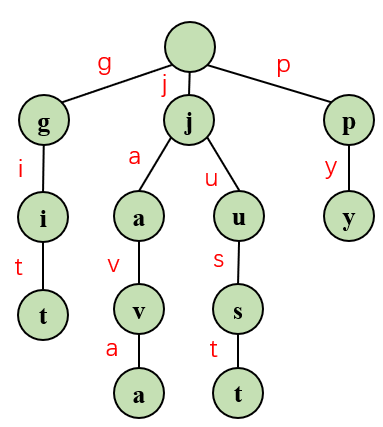
字典树不同于其他树结构,一般的树结构存储都是将整个字符串全部存储在一个节点上,但是字典树就不是这样,它是下面这种结构:
外形有点像门帘,每一个节点只存储一个字符。一共存储了四个单词git, java,just,py。我们现在可以明白了,我们想要查询那个单词只需要遍历单词的长度即可。
那么节点里面应该包含那些内容呢,首先要存储的字符,而且要包含指向26个字母的指针,因为我们英文单词只包含26个英文字母(不考虑大小写或者其他特殊情况),所以我们需要指针来指向它们。
class Node{
char c; //基本信息
Node next[26]; //指向下一个节点的指针
}但实际情况我们需要很多类型的字符串需要存储,类似于网址,邮箱等等,包含一些特殊字符,而且实际情况中,有些单词并不会出现,所以固定保存类型不符合实际情况。那么我们就需要具有动态性。
class Node{
char c; //基本信息
Map<char, Node> next; //使用Map动态指向下一个节点信息
} 其实在上面的结构中,我还可以进行优化,其实在每一个节点信息中,我们已经知道了指向下一个节点的字符信息,我们并不需要另外设置char c;来保存字符。Map中其实已经保存了下一个节点的字符。
class Node{
Map<char, Node> next; //使用Map动态指向下一个节点信息
} 但是还有一个问题就是,我们怎么区分字符串结束,类似git和github完全不是一个意思,如果按照上面的存储方式,github就会覆盖git。这样也就达不到我们的目的了,所以说,我们在节点上还需要多存储一个信息,就是bool变量 isWord 。
class Node{
boolean isWord;
Map<char, Node> next; //使用Map动态指向下一个节点信息
}构造函数比较简单,我们只需要初始化有一个根节点,这个节点只存储指向下个节点的信息。
public Trie() {
root = new Node();
size = 0;
}向字典树中添加元素,就是将字符串中一个一个字符提取出来,然后添加到树中,对于不存在的节点,就像Map中添加,对于存在的则向下移动,最后对最后一个更新isWord,保证是一个字符串的结束。
遍历实现:
public void add(String word) {
Node cur = root;
for (int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
if (cur.next.get(c) == null)
cur.next.put(c, new Node());
cur = cur.next.get(c);
}
if (!cur.isWord) {
cur.isWord = true;
size++;
}
}递归实现:
public void add(String word) {
add(root, word);
}
private void add(Node node, String word) {
if (word.length() == 0) {
if (!node.isWord){
node.isWord = true;
size++;
}
return;
}
char c = word.charAt(0);
if (node.next.get(c) == null)
node.next.put(c, new Node());
add(node.next.get(c), word.substring(1));
}在最开始就已经说到了查询操作,我们也需要对待查询的字符串进行拆解,然后不断再树中进行查找,如果找不到相应的节点就返回false。必须完全匹配并且最后一个节点的isWord是True才可以。
遍历实现:
public boolean contains(String word) {
Node cur = root;
for (int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
if (cur.next.get(c) == null)
return false;
cur = cur.next.get(c);
}
return cur.isWord;
}递归实现:
public boolean contains(String word) {
return contains(root, word);
}
private boolean contains(Node node, String word) {
if (word.length() == 0)
return node.isWord;
if (node == null)
return false;
return contains(node.next.get(word.charAt(0)), word.substring(1));
}前缀搜索就是查询这一个树结构包含不包含这个前缀,其实和查询操作相同,只不过在最后不检查isWord;直接返回True就好。
遍历实现:
public boolean isPrefix(String prefix) {
Node cur = root;
for (int i = 0; i < prefix.length(); i++) {
char c = prefix.charAt(i);
if (cur.next.get(c) == null)
return false;
cur = cur.next.get(c);
}
return true;
}递归实现:
public boolean isPrefix(String word) {
return contains(root, word);
}
private boolean isPrefix(Node node, String word) {
if (word.length() == 0)
return true;
if (node == null)
return false;
return contains(node.next.get(word.charAt(0)), word.substring(1));
}更多精彩内容,大家可以转到我的主页:曲怪曲怪的主页
或者关注我的微信公众号:TeaUrn
或者扫描下方二维码进行关注。里面有惊喜等你哦。
源码地址:可在公众号内回复 数据结构与算法源码 即可获得。