- Paper link: https://arxiv.org/pdf/2006.07988.pdf
- Author's code repo:https://github.com/jianhao2016/GPRGNN. Note that the original code is implemented with PyTorch for the paper.
Run with following (available dataset: "cora", "citeseer", "pubmed", "computers", "photo", "squirrel", "chameleon", "cornell", "texas")
sh Reproduce_GPRGNN.sh| Cora | Citeseer | PubMed | Computers | Photo | Chameleon | Squirrel | Texas | Cornell | |
|---|---|---|---|---|---|---|---|---|---|
| Tensorflow | 79.08 | 65.96 | 83.74 | 83.44 | 92.06 | 67.61 | 51.82 | 88.02 | 85.25 |
| Paddle | |||||||||
| Origin | 79.51 | 67.63 | 85.07 | 82.90 | 91.93 | 67.48 | 49.93 | 92.92 | 91.36 |
GPRConv
In file layers/conv/gpr_conv.py
The basic structure is similar to gcn_conv.py
- Provides the GPR-GNN conv layer
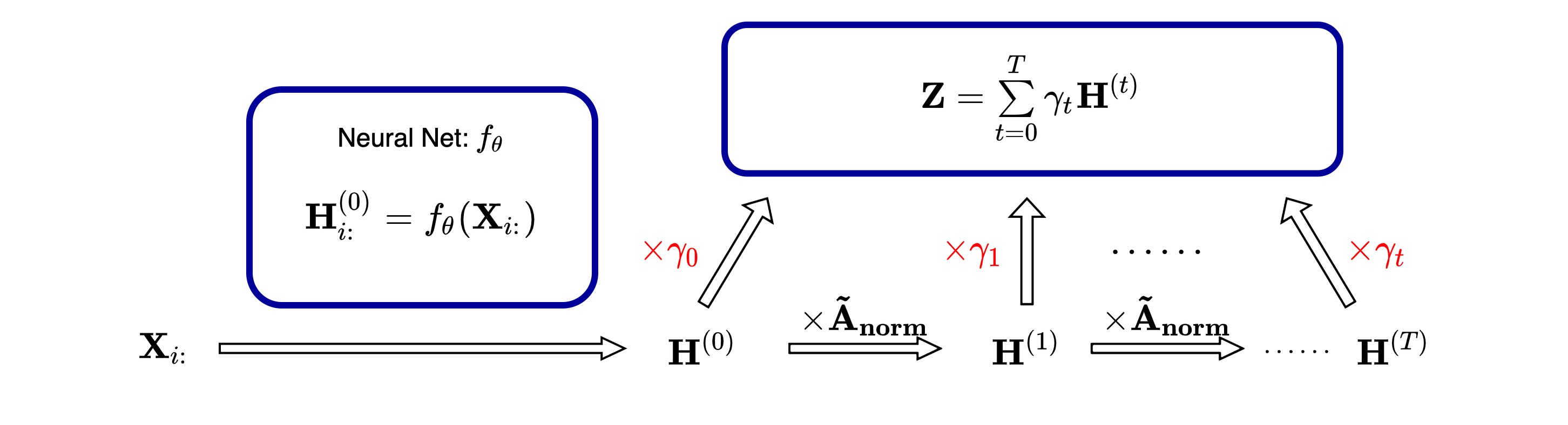
- In
__init__method: Add the initialization for learnt weights$\gamma_k$ and define the steps of propagation$K$ - For initializaiton method provided:
-
$\textbf{SGC}$ :$\gamma_k = \delta_{kK}$ , weight for the last layer is set to$1$ , others as$0$ ; -
$\textbf{PPR}$ :$\gamma_k=\alpha(1-\alpha)^{k}\text{ for } k<K \text{ and }\gamma_K=(1-\alpha)^K$ ; -
$\textbf{NPPR}$ :$\gamma_k=\alpha^{k} / \sum\limits_{k=0}^{K}\alpha^{k}$ ; -
$\textbf{Random}$ :$\gamma\sim 2\sqrt{\frac{K+1}{3}}\mathbf{U}(-\sqrt{\frac{3}{K+1}},\sqrt{\frac{3}{K+1}})$ -
$\textbf{WS}$ : User defined initial value for$\gamma_k$
-
- For
$K$ : recommended value is 10 (proposed by GPR-GNN origin paper)
- For initializaiton method provided:
- In
reset_parametersmethod: Use$\textbf{PPR}$ initializaiton method to reset parameters
GPRGNNModel
In file models/gprgnn.py
- Provides the complete GPR-GNN model
- In
__init__method: besides basic dimension information of node features and num of classes, GPR related hyperparameters ($K$ ,$\textbf{Init}$ ,$\alpha$ ,$\text{dprate}$ , etc.) are also transfered to the network - In
forwardpropagation:- After feature extraction, it passes a special dropout layer controled by
$\text{dprate}$ before entering propagation layers. - Then, those representations of nodes are transferred into
GPRConv
- After feature extraction, it passes a special dropout layer controled by
NormalizeFeatures
In file transforms/normalize_features.py
- Provides a row-wise normalization for feature matrix
In file examples/gprgnn/gprgnn_trainer.py
- Function
random_planetoid_splitsis defined to randomly split dataset and ensure the numbers of nodes from each classes are the same in training set. - Maximum of epoches is set as 1000 and early stopping trick is applied.
- Early stopping mechanism is used.
In file examples/gprgnn/Reproduce_GPRGNN.sh
-
To keep the same with experiments in origin paper,5 homophily graph datasets,
Cora,Citeseer,PubMed,ComputersandPhoto, adopt sparse split$(2.5%/2.5%/95%)$ for (training/validation/test), and 4 heterophily graph datasets,Chameleon,Squirrel,TexasandCornell, adopt dense split$(60%/20%/20%)$ . -
Train model with each hyperparameter setting for 10 times and calculate the average accuracy.
-
Best hyperparameters for different datasets are given in the file.
In file examples/gprgnn/test.accuracy
| Cora | Citeseer | PubMed | Computers | Photo | Chameleon | Squirrel | Texas | Cornell | |
|---|---|---|---|---|---|---|---|---|---|
| Tensorflow | 79.08 | 65.96 | 83.74 | 83.44 | 92.06 | 67.61 | 51.82 | 88.02 | 85.25 |
| Paddle | |||||||||
| Origin | 79.51 | 67.63 | 85.07 | 82.90 | 91.93 | 67.48 | 49.93 | 92.92 | 91.36 |
- Test accuracy on
TexasandCornellis unstable, fluctuating from 75 ~ 95.